
⑴ ;⑵
;⑶
不具有奇偶性(4)
的单调增区间是
(5)可能存在经过点
的直线与函数的图象不相交
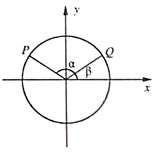
(I)求 ;
(Ⅱ)若 ,求
.
| 距消防站距离 | 1.8 | 2.6 | 3.1 | 4.3 | 5.5 | 6.1 |
| 火灾损失费用 | 17.8 | 19.6 | 27.5 | 31.3 | 36.0 | 43.2 |
如果统计资料表明 与
有线性相关关系,试求(解答过程中,各种数据都精确到0.01)
(I)相关系数 ;
(Ⅱ)线性回归方程;
(Ⅲ)若发生火灾的某居民区与最近的消防站相距10.0千米,评估一下火灾的损失.
参考数据: ,
,
,
参考公式:相关系数
回归方程 中斜率和截距的最小二乘法估计公式分别为:
,
.

(I)求 的解析式及对称中心坐标;
(Ⅱ)将 的图象向右平移
个单位,再将横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数
的图象,求函数
在
上的单调区间及最值.

(I)求 的值;
(Ⅱ)求被调查的市民的满意程度的平均数,众数,中位数;
(Ⅲ)若按照分层抽样从 ,
中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在
的概率.