浙江省绍兴市柯桥区柯桥钱清初中2020届九年级上学期数学10...

更新时间：2019-12-11 浏览次数：277 类型：月考试卷

一、单选题

1. (2019九上·柯桥月考) 抛物线 $\text{[math]}$ 的顶点坐标是（）

A . (3，1) B . (3，－1) C . (－3，1) D . (－3，－1)

答案解析收藏纠错 + 选题
2. (2019九上·柯桥月考) 将抛物线 $\text{[math]}$ 向右平移3个单位后所得抛物线的解析式为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2019九上·柯桥月考)
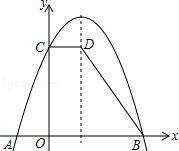
某公园一喷水池喷水时水流的路线呈抛物线（如图）．若喷水时水流的高度y（m）与水平距离x（m）之间的函数关系式是y=﹣x²+2x+1.25，则水池在喷水过程中水流的最大高度为（　　）

A . 1.25米 B . 2.25米 C . 2.5米 D . 3米

答案解析收藏纠错 + 选题
4. (2019九上·柯桥月考) 如图所示的暗礁区，两灯塔A，B之间的距离恰好等于圆的半径，为了使航船（S）不进入暗礁区，那么S对两灯塔A，B的视角∠ASB必须（）

A . 大于60° B . 小于60° C . 大于30° D . 小于30°

答案解析收藏纠错 + 选题
5. (2019九上·柯桥月考) 若二次函数 $\text{[math]}$ 的图象的对称轴在y轴的右侧，则实数m的取值范围是 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2019九上·柯桥月考) 如图，在Rt△ABC中，∠ACB=90°，AC=3，AB=5，CD是斜边AB上的中线，以AC为直径作O，设线段CD的中点为P，则点P与O的位置关系是（）

A . 点P在O外 B . 点P在O上 C . 点P在O内 D . 无法确定

答案解析收藏纠错 + 选题
7. (2019九上·柯桥月考) 若二次函数y＝ax²+bx+c（a＜0）的图象经过点（2，0），且其对称轴为x＝﹣1，则使函数值y＞0成立的x的取值范围是（）

A . ﹣4≤x≤2 B . x＜﹣4或x＞2 C . x≤﹣4或x≥2 D . ﹣4＜x＜2

答案解析收藏纠错 + 选题
8. (2020九上·诸城期末) 如图，⊙O的半径为5，△ABC是⊙O的内接三角形，连接OB、OC.若∠BAC与∠BOC互补，则弦BC的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2019九上·柯桥月考) 已知点（x₀ ， y₀）是二次函数y=ax²+bx+c（a＜0）的一个点，且x₀满足关于x的方程2ax+b=0，则下列选项正确的是（）

A . 对于任意实数x都有y≥y₀ B . 对于任意实数x都有y≤y₀ C . 对于任意实数x都有y＞y₀ D . 对于任意实数x都有y＜y₀

答案解析收藏纠错 + 选题
10. (2019九上·柯桥月考) 一个滑道由滑坡（AB段）和缓冲带（BC段）组成，如图所示，滑雪者在滑坡上滑行的距离y（单位：m）和滑行时间t₁（单位：s）满足二次函数关系，并测得相关数据：

滑行时间t₁/s

0

1

2

3

4

滑行距离y₁/s

0

4.5

14

28.5

48

滑雪者在缓冲带上滑行的距离y₂（单位：m）和在缓冲带上滑行时间t₂（单位：s）满足：y₂＝52t₂﹣2t₂² ，滑雪者从A出发在缓冲带BC上停止，一共用了23s，则滑坡AB的长度（）米

A . 270 B . 280 C . 375 D . 450

答案解析收藏纠错 + 选题

二、新添加的题型

11. (2019九上·柯桥月考) 如图，AB为 $\text{[math]}$ 的直径，CD为 $\text{[math]}$ 的弦，∠BCD=34°，则∠ABD=.

答案解析收藏纠错 + 选题

三、填空题

12. (2019九上·宜春月考) 如果抛物线y=（m﹣1）x²的开口向上，那么m的取值范围是．

答案解析收藏纠错 + 选题
13. (2020九上·镇海期中) 工程上常用钢珠来测量零件上小圆孔的宽口，假设钢珠的直径是10mm，测得钢珠顶端离零件表面的距离为8mm，如图所示，则这个小圆孔的宽口AB的长度为mm．

答案解析收藏纠错 + 选题
14. (2022·舟山模拟) 如图，在平面直角坐标系中，菱形OABC的顶点A在 $\text{[math]}$ 轴正半轴上，顶点C的坐标为（4，3），D是抛物线 $\text{[math]}$ 上一点，且在 $\text{[math]}$ 轴上方，则△BCD面积的最大值为.

答案解析收藏纠错 + 选题
15. (2020九上·招远期末)
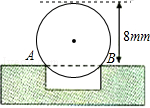
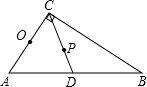
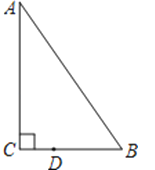
如图，△ABC中，已知∠C=90°，∠B=55°，点D在边BC上，BD=2CD．把△ABC绕着点D逆时针旋转m（0＜m＜180）度后，如果点B恰好落在初始Rt△ABC的边上，那么m= ．

答案解析收藏纠错 + 选题
16. (2019九上·柯桥月考) 如图，在平面直角坐标系中，已知点A（0，1）、点B（0，1+t）、C（0，1﹣t）（t＞0），点P在以D（3，5）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则t的最小值是.

答案解析收藏纠错 + 选题

四、解答题

17. (2019九上·柯桥月考) 如图，已知△ABC中，AC=6，∠ABC=45°.
1. （1）用直尺和圆规作出△ABC的外接圆（保留作图痕迹，写出结论，不写画法）；
2. （2）求出△ABC的外接圆半径.
答案解析收藏纠错 + 选题
18. (2019九上·柯桥月考) 已知二次函数y＝－x²＋4x.
1. （1）用配方法把该函数化为y＝a(x－h)²＋k的形式；
2. （2）求该函数图象的对称轴和顶点坐标.
答案解析收藏纠错 + 选题
19. (2019九上·柯桥月考) 如图，已知抛物线y=ax²+bx+3与x轴交于A、B两点，过点A的直线l与抛物线交于点C，其中A点的坐标是（1，0），C点坐标是（4，3）.
1. （1）求抛物线的解析式；
2. （2）设直线l与y轴交于点D，抛物线交y轴于点E，则△DBE的面积是多少？
答案解析收藏纠错 + 选题
20. (2019九上·柯桥月考) 已知：如图，抛物线y=﹣x²+bx+c与x轴交于点A（﹣1，0），B（3，0），与y轴交于点C.过点C作CD∥x轴，交抛物线的对称轴于点D.
1. （1）求该抛物线的解析式；
2. （2）若将该抛物线向下平移m个单位，使其顶点落在D点，求m的值.
答案解析收藏纠错 + 选题
21. (2019九上·柯桥月考) 定义：若△ABC中，其中一个内角是另一个内角的一半，则称△ABC为“半角三角形”.
1. （1）若Rt△ABC为半角三角形，∠A=90°，则其余两个角的度数为.
2. （2）如图，以△ABC的边AB为直径画圆，与边AC交于M，与边BC交于N，已知CN= $\text{[math]}$ AC
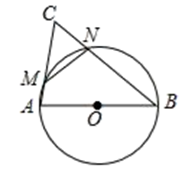
  ①求证：∠C=60°.
  
  ②若△ABC是半角三角形，求∠B的度数.
答案解析收藏纠错 + 选题
22. (2019九上·柯桥月考) 某景区内有一块矩形油菜花田地（数据如图示，单位：m.）
现在其中修建一条观花道（图中阴影部分）供游人赏花.设改造后剩余油菜花地所占面积为ym².
1. （1）求y与x的函数表达式；
2. （2）若改造后观花道的面积为13m² ，求x的值；
3. （3）若要求 0.5≤ x ≤1，求改造后剩余油菜花地所占面积的最大值.
答案解析收藏纠错 + 选题
23. (2020九上·台州月考) 已知P是⊙O上一点，过点P作不过圆心的弦PQ，在劣弧PQ和优弧PQ上分别有动点A、B(不与P，Q重合)，连接AP、BP.若∠APQ=∠BPQ.
1. （1）如图1，当∠APQ=45°，AP=1，BP=2 $\text{[math]}$ 时，求⊙O的半径；
2. （2）如图2，选接AB，交PQ于点M，点N在线段PM上(不与P、M重合)，连接ON、OP，若∠NOP+2∠OPN=90°，探究直线AB与ON的位置关系，并证明.
答案解析收藏纠错 + 选题
24. (2019九上·柯桥月考) 如图，抛物线 $\text{[math]}$ 与x轴交于A（-1，0），B（5，0）两点，直线 $\text{[math]}$ 与y轴交于点C，与x轴交于点D。点P是x轴上方的抛物线上一动点，过点P作PF⊥x轴与点F，交直线CD于点E。设点P的横坐标为m。
1. （1）求抛物线的解析式；
2. （2）若PF=5EF，求m的值.
答案解析收藏纠错 + 选题