 B .
B .  C .
C .  D .
D . 

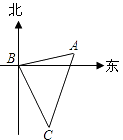
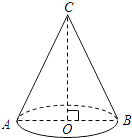
如图,客轮在海上以30km/h的速度由B向C航行,在B处测得灯塔A的方向角为北偏东80°,测得C处的方向角为南偏东25°,航行1小时后到达C处,在C处测得A的方向角为北偏东20°,则C到A的距离是( )
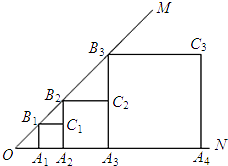
如图,已知动点P在函数y= (x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=﹣x+1交于点E,F,则AF•BE的值为( )

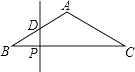
如图,已知△ABC中,AB=AC=2,∠B=30°,P是BC边上一个动点,过点P作PD⊥BC,交△ABC的AB边于点D.若设PD为x,△BPD的面积为y,则y与x之间的函数关系的图象大致是( )
 B .
B . 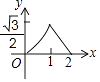 C .
C . 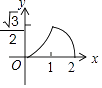 D .
D . 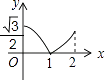
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
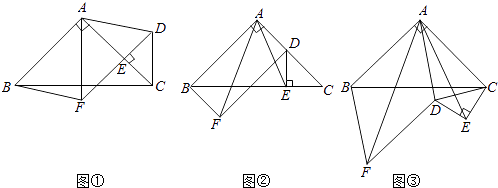
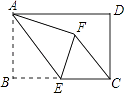
如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.