一、选择题(本大题10小题,每小题3分,共30分)
-
-
A . (-2,3)
B . (2,-3)
C . (-2,-3)
D . (-3,-2)
-
A . a≠1
B . a>1
C . a<1
D . a≠0
-
A . (3,1)
B . (3,-1)
C . (-3,1)
D . (-3,-1)
-
A . 2
B . -2
C . 2或-2
D . 4
-
A . y=x2+1
B . y=x2+3
C . y=(x-1)2+2
D . y=(x+1)2+2
-
A . 有两个不相等的实数根
B . 有两个相等的实数根
C . 无实数根
D . 不确定
-
-
9.
(2019九上·韶关期中)
如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m为( )
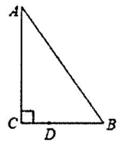
A . 70°
B . 70°或120°
C . 120°
D . 80°
-
10.
(2019九上·韶关期中)
二次函数y=ax
2+bc(a≠0)的部分图象如图,图象过点(-1,0), 对称轴为直线x=2,下列结论:①抛物线与x轴的另一个交点是(5,0); ②4a-2b+c>0:③4a+b=0;④当x>-1时,y的值随κ值的增大而增大。其中正确的结论有( )
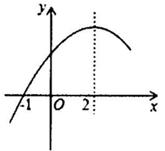
A . 1个
B . 2个
C . 3个
D . 4个
二、填空题(本大题6小题,每小题4分,共24分)
-
-
-
-
-
15.
(2019九上·韶关期中)
如右图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD, △ABD绕点A旋转后得到△ACE,则CE的长度为
。
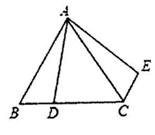
-
三、解答题(一)(本大题3小题,每小题6分,共18分)
-
-
-
(1)
求出抛物线y=x2-2x-8图象的顶点坐标及对称轴
-
(2)
若抛物线与x轴的两个交点分别为A、B,求线段AB的长。
-
-
(1)
作出△ABC关于原点对称的图形△A1B1C1;
-
四、解答题(二)(本大题3小题,每小题7分,共21分)
-
20.
(2019九上·江油月考)
某省为解决农村饮用水问题,省财政部门共投资10亿元对各市的农村饮用水的“改水工程”予以一定比例的补助.2012年,A市在省财政补助的基础上投入600万元用于“改水工程”,计划以后每年以相同的增长率投资,2014年该市计划投资“改水工程”864万元。
-
-
(2)
从2012年到2014年,A市三年共投资“改水工程”多少万元?
-
21.
(2019九上·韶关期中)
在△AMB中,∠AMB=90°,将△AMB以B为中心顺时针旋转90°,得到△CNB.
求证:AM∥NB.

-
-
-
(2)
设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
五、解答题(三)(本大题3小时,每小题9分,共27分)
-
23.
(2019九上·韶关期中)
某商品的进价为每件40元,当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
-
(1)
若设每件降价x元、每星期售出商品的利润为y元,请写y与x函数关系式,并求出自变量x的取值范围
-
(2)
当降价多少元时,每星期的利润最大?最大利润是多少元?
-
24.
(2019九上·韶关期中)
四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF。
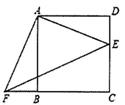
-
-
(2)
△ABF可以由△ADE绕旋转中心点,按顺时针方向旋转度得到;
-
-
-
-
(2)
P为抛物线上的点,且满足S△PAB=8,求P点的坐标
-
(3)
设抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由。
 B .
B .  C .
C . 




