2017年河南省南阳市淅川县中考数学二模试卷

更新时间：2017-07-26 浏览次数：998 类型：中考模拟

一、选择题

1. (2022七上·雷州期中) 下列各数中，最大的数是（）

A . |﹣3| B . ﹣2 C . 0 D . 1

答案解析收藏纠错 + 选题
2. (2017·淅川模拟) 下列运算正确的是（）

A . a•a³=a³ B . （ab）³=a³b C . （a³）²=a⁶ D . a⁸÷a⁴=a²

答案解析收藏纠错 + 选题
3. (2018·吉林模拟) 如图所示正三棱柱的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2019八下·镇平期末) 甲、乙、丙、丁四人进行射击测试，每人10次射击成绩的平均数都均为8.8环，方差分别为S_甲²=0.63，S_乙²=0.51，S_丙²=0.48，S_丁²=0.42，则四人中成绩最稳定的是（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
5. (2017·淅川模拟) 已知扇形的圆心角为45°，半径长为12，则该扇形的弧长为（）

A . $\text{[math]}$ B . 2π C . 3π D . 12π

答案解析收藏纠错 + 选题
6. (2023九上·阿克苏月考) 如图，过正五边形ABCDE的顶点A作直线l∥BE，则∠1的度数为（）

A . 30° B . 36° C . 38° D . 45°

答案解析收藏纠错 + 选题
7. (2020九上·无棣期末)
如图，点A是反比例函数y= $\text{[math]}$ 的图象上的一点，过点A作AB⊥x轴，垂足为B．点C为y轴上的一点，连接AC，BC．若△ABC的面积为3，则k的值是（　　）

A . 3 B . ﹣3 C . 6 D . ﹣6

答案解析收藏纠错 + 选题
8. (2017·淅川模拟) 如图，△ABC内接于半径为5的⊙O，圆心O到弦BC的距离等于3，则∠A的正切值等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2017·淅川模拟) 从标有号数1到10的10张卡片中，随意抽取一张，其号数为3的倍数的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 无法确定

答案解析收藏纠错 + 选题
10. (2017·淅川模拟)
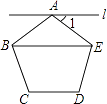
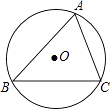
如图①，四边形ABCD中，BC∥AD，∠A=90°，点P从A点出发，沿折线AB→BC→CD运动，到点D时停止，已知△PAD的面积s与点P运动的路程x的函数图象如图②所示，则点P从开始到停止运动的总路程为（）

A . 4 B . 2+ $\text{[math]}$ C . 5 D . 4+ $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2019·河南模拟) 计算：2^﹣²﹣ $\text{[math]}$ =．

答案解析收藏纠错 + 选题
12. (2017·淅川模拟) 如图，平面上直线a，b分别经过线段OK两端点（数据如图），则a，b相交所成的锐角是．

答案解析收藏纠错 + 选题
13. (2017·淅川模拟) 如图，在等腰Rt△OAA₁中，∠OAA₁=90°，OA=1，以OA₁为直角边作等腰Rt△OA₁A₂ ，以OA₂为直角边作等腰Rt△OA₂A₃ ， …则OA₆的长度为．

答案解析收藏纠错 + 选题
14. (2017·淅川模拟) 二次函数y=ax²+bx+c（a≠0）的图象如图所示，下列结论：①2a+b=0；②a+c＞b；③抛物线y=ax²+bx+c与x轴的另一个交点为（3，0）；④abc＞0．其中正确的结论是（填写序号）

答案解析收藏纠错 + 选题
15. (2017·淅川模拟) 如图，在平行四边形ABCD中，AB=6，BC=4，∠B=60°，点E是边AB上的一点，点F是边CD上一点，将平行四边形ABCD沿EF折叠，得到四边形EFGC，点A的对应点为点C，点D的对应点为点G，则△CEF的面积．

答案解析收藏纠错 + 选题

三、解答题

16. (2017·唐河模拟) 先化简，再求值： $\text{[math]}$ ÷ $\text{[math]}$ ，其中m是方程x²+2x﹣3=0的根．

答案解析收藏纠错 + 选题
17. (2017·淅川模拟) 为实施“农村留守儿童关爱计划”，某校对全校各班留守儿童的人数情况进行了统计，发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况，并制成了如下两幅不完整的统计图：
1. （1）将该条形统计图补充完整；
2. （2）求该校平均每班有多少名留守儿童？
3. （3）某爱心人士决定从只有2名留守儿童的这些班级中，任选两名进行生活资助，请用列表法或画树状图的方法，求出所选两名留守儿童来自同一个班级的概率．
答案解析收藏纠错 + 选题
18. (2017·淅川模拟) 如图，AB是半圆O的直径，点C是半圆O上一点，∠COB=60°，点D是OC的中点，连接BD，BD的延长线交半圆O于点E，连接OE，EC，BC．
1. （1）求证：△BDO≌△EDC．
2. （2）若OB=6，则四边形OBCE的面积为．
答案解析收藏纠错 + 选题
19. (2017·淅川模拟) 为解决江北学校学生上学过河难的问题，乡政府决定修建一座桥，建桥过程中需测量河的宽度（即两平行河岸AB与MN之间的距离）．在测量时，选定河对岸MN上的点C处为桥的一端，在河岸点A处，测得∠CAB=30°，沿河岸AB前行30米后到达B处，在B处测得∠CBA=60°，请你根据以上测量数据求出河的宽度．（参考数据： $\text{[math]}$ ≈1.41， $\text{[math]}$ ≈1.73，结果保留整数）

答案解析收藏纠错 + 选题
20. (2017·淅川模拟) 某小区为了绿化环境，计划分两次购进A、B两种花草，第一次分别购进A、B两种花草30棵和15棵，共花费675元；第二次分别购进A、B两种花草12棵和5棵．两次共花费940元（两次购进的A、B两种花草价格均分别相同）．
1. （1） A、B两种花草每棵的价格分别是多少元？
2. （2）若购买A、B两种花草共31棵，且B种花草的数量少于A种花草的数量的2倍，请你给出一种费用最省的方案，并求出该方案所需费用．
答案解析收藏纠错 + 选题
21. (2017·淅川模拟)
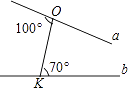
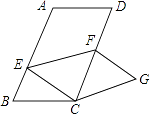
如图，在平面直角坐标系xOy中，矩形OEFG的顶点E的坐标为（4，0），顶点G的坐标为（0，2），将矩形OEFG绕点O逆时针旋转，使点F落在y轴的点N处，得到矩形OMNP，OM与GF交于点A．
1. （1）求图象经过点A的反比例函数的解析式；
2. （2）设（2）中的反比例函数图象交EF于点B，直接写出直线AB的解析式．
答案解析收藏纠错 + 选题
22. (2017·淅川模拟) 在△ABC中，∠ACB是锐角，点D在射线BC上运动，连接AD，将线段AD绕点A逆时针旋转90°，得到AE，连接EC．
1. （1）
  操作发现：
  若AB=AC，∠BAC=90°，当D在线段BC上时（不与点B重合），如图①所示，请你直接写出线段CE和BD的位置关系和数量关系是，；
2. （2）
  猜想论证：
  在（1）的条件下，当D在线段BC的延长线上时，如图②所示，请你判断（1）中结论是否成立，并证明你的判断．
3. （3）
  拓展延伸：
  如图③，若AB≠AC，∠BAC≠90°，点D在线段BC上运动，试探究：当锐角∠ACB等于度时，线段CE和BD之间的位置关系仍成立（点C、E重合除外）？此时若作DF⊥AD交线段CE于点F，且当AC=3 $\text{[math]}$ 时，请直接写出线段CF的长的最大值是
答案解析收藏纠错 + 选题
23. (2017·淅川模拟)
如图，抛物线y=﹣x²+bx+c经过A（﹣1，0），C（0，4）两点，与x轴交于另一点B，
1. （1）求抛物线的解析式；
2. （2）求P在第一象限的抛物线上，P点的横坐标为t，过点P向x轴做垂线交直线BC于点Q，设线段PQ的长为m，求m与t之间的函数关系式并求出m的最大值；
3. （3）在（2）的条件下，抛物线上一点D的纵坐标为m的最大值，连接BD，在抛物线是否存在点E（不与点A，B，C重合）使得∠DBE=45°？若不存在．请说明理由；若存在请求E点的坐标．
答案解析收藏纠错 + 选题