一、单项选择题(共10个小题,每小题3分,满分30分)
-
-
A . 任意购买一张电影票,座位号是奇数
B . 明天晚上会看到太阳
C . 五个人分成四组,这四组中有一组必有2人
D . 三天内一定会下雨
-
A . m<-4
B . m≠0
C . m≠-4
D . m>-4
-
A . y=-3x2-2
B . y=-3(x-2)2
C . y=-3x2+2
D . y=-3(x+2)2
-
5.
(2020九上·中山期末)
某鱼塘里养了100条鲤鱼、若干条草鱼和50条罗非鱼,通过多次捕捞实验后发现,捕捞到草鱼的频率稳定在0.5左右,可估计该鱼塘中草鱼的数量为( )
A . 150
B . 100
C . 50
D . 200
-
A . c<  B . c<
B . c<  C . c>
C . c>  D . c>
D . c> 
-
A . a<  或a>1
B . a<
或a>1
B . a<  C .
C .  <a<1
D . a>1
<a<1
D . a>1
-
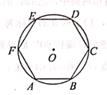
A . 50°
B . 55°
C . 65°
D . 70°
-
-
10.
(2020九上·中山期末)
如图是二次函数y=ax
2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③3方程ax
2+bx+c=0的两根分别为-3和1:④当x<1时,函数值y<0.其中正确的命题是
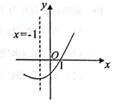
A . ②③
B . ①③
C . ①②
D . ①③④
二、填空题(共7个小题,每小题4分,满分28分)
-
-
-
-
14.
(2020九上·中山期末)
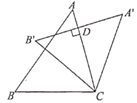
如图,把△ABC绕点C顺时针旋转得到△ABC,此时AB⊥AC于点D,已知∠A=50°,则∠BCB
’的度数是
。
-
15.
(2020九上·中山期末)
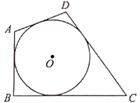
如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=15,则四边形ABCD的周长为
。
-
16.
(2020九上·中山期末)
小强推铅球时,铅球的高度y(m)与水平行进的距离x(m)之间的关系为y=

(x-4)
2+3,则小强推铅球的成绩是
m。
-
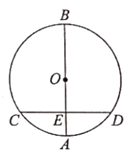
17.
(2020九上·中山期末)
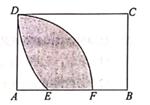
如图,以矩形ABCD的顶点A为圆心,线段AD长为半径画弧,交AB边于点F;再以顶点C为圆心,线段CD长为半径画弧,交AB边于点E,若AD=

,CD=2,则

、

和EF围成的阴影部分面积是
。
三、解答题(一)(共3个小题,每小题6分,满分18分)
-
-
19.
(2020九上·中山期末)
如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(-4,1),点B的坐标为(-1,1)

-
(1)
画出△ABC绕点B逆时针旋转90°后得到的△A1BC1;
-
(2)
画出△ABC关于原点O对称的△A2B2C2。
-
四、解答题(二)(共3个小题,每小题8分,满分24分)
-
21.
(2020九上·中山期末)
甲和乙玩一个游戏:三张大小、质地都相同的卡片上分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下,甲从中任意抽取一张,记下数字后放回洗匀,然后乙从中任意抽取一张,计算甲和乙抽得的两个数字之和,若和为奇数,则甲胜;若和为偶数,则乙胜。
-
(1)
请你用画树状图或列表的方法,求出这两数和为6的概率;
-
(2)
你认为这个游戏规则对双方公平吗?说明你的理由。
-
-
-
(2)
若抛物线与直线y=x+k2-1的一个交点在y轴上,求该二次函数的顶点坐标。
-
23.
(2020九上·中山期末)
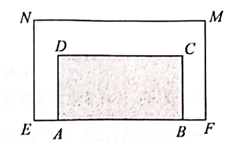
如图,有一块长方形的空地MNEF,现准备在长方形ABCD的区域种草,使得草地的面积占整个空地面的一半,其中AB=24m,BC=12m,AE=BF,MN与CD的距离是AE的1.5倍,求空地的长和宽。
五、解答题(三)(共2个小题,每小题10分,满分20分)
-
24.
(2020九上·中山期末)
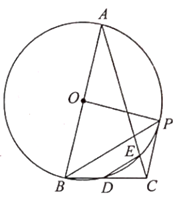
如图,在△ABC中,AB=AC,∠A=30°,AB=10,以AB为直径的⊙O交BC于点D交AC于点E,连接DE,过点B作BP平行于DE,交⊙O于点P,连接CP、OP。
-
-
(2)
求

的长度;
-
-
25.
(2020九上·中山期末)
如图,抛物线y=ax
2-

x+c与x轴相交于点A(-2,0)、B(4,0),与y轴相交于点C,连接AC、BC,以线段BC为直径作⊙M,过点C作直线CE∥AB,与抛物线和⊙M分别交于点D、E,点P在BC下方的抛物线上运动。

-
-
(2)
当△PDE是以DE为底边的等腰三角形时,求点P的坐标;
-
(3)
当四边形ACPB的面积最大时,求点P的坐标并求出最大值。
 B .
B . 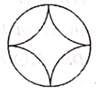 C .
C .  D .
D .