河南省信阳市2019届九年级普通高中招生模拟考试（一）数学试...

更新时间：2024-07-13 浏览次数：243 类型：中考模拟

一、单选题

1. (2021·湖南模拟) 实数 $\text{[math]}$ 在数轴上对应的点的位置如图所示，这四个数中最大的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2019·信阳模拟) 2018年4月10日，历时四个月的“2018中国茶叶区域公用品牌价值评估”结果出炉，信阳毛尖较去年增加3.61亿元，以63.52亿元蝉联品牌价值排行榜第二名，并被评选为“最具品牌带动力”的三大品牌之一.数据63.52亿元用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024七上·桦甸期末) 如图，是一个正方体的表面展开图，则原正方体中“学”字所在的面相对的面上标的字是（）

A . 我 B . 是 C . 优 D . 生

答案解析收藏纠错 + 选题
4. (2019·信阳模拟) 下列运算正确的是

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2019·沈丘模拟) 如图所示是小明在某条道路所统计的某个时段来往车辆的车速情况，下列说法中正确的是（）

A . 中位数是52.5 B . 众数是8 C . 众数是52 D . 中位数是53

答案解析收藏纠错 + 选题
6. (2019·信阳模拟) “算经十书”是指汉唐一千多年间的十部著名数学著作，它们曾经是隋唐时期国子监算学科的教科书，这些流传下来的古算书中凝聚着历代数学家的劳动成果．下列四部著作中，不属于我国古代数学著作的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2020九上·定陶期末) 关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 没有实数根，则整数 $\text{[math]}$ 的最小值是（）

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题
8. (2024九下·大洼模拟) 点P的坐标是（m，n），从﹣5，﹣3，0，4，7这五个数中任取一个数作为m的值，再从余下的四个数中任取一个数作为n的值，则点P（m，n）在平面直角坐标系中第二象限内的概率是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2019·信阳模拟) 如图，在平面直角坐标系中，以O为圆心，适当长为半径画弧，交x轴于点M，交y轴于点N，再分别以点M、N为圆心，大于 $\text{[math]}$ MN的长为半径画弧，两弧在第二象限交于点P.若点P的坐标为（2x，y+1），则y关于x的函数关系为（　　）

A . y=x B . y=﹣2x﹣1 C . y=2x﹣1 D . y=1﹣2x

答案解析收藏纠错 + 选题
10. (2021九上·惠州月考) 如图是二次函数y=ax²+bx+c（a，b，c是常数，a≠0）图象的一部分，与x轴的交点A在点（2，0）和（3，0）之间，对称轴是x=1．对于下列说法：①ab＜0；②2a+b=0；③3a+c＞0；④a+b≥m（am+b）（m为实数）；⑤当﹣1＜x＜3时，y＞0，其中正确的是（）

A . ①②④ B . ①②⑤ C . ②③④ D . ③④⑤

答案解析收藏纠错 + 选题

二、填空题

11. (2019·信阳模拟) 计算： $\text{[math]}$ 。

答案解析收藏纠错 + 选题
12. (2019·信阳模拟) 如图，在平行线 $\text{[math]}$ 之间放置一块直角三角板，三角板的锐角顶点 $\text{[math]}$ 分别在直线 $\text{[math]}$ 上，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是.

答案解析收藏纠错 + 选题
13. (2020·广东模拟) 如果不等式组 $\text{[math]}$ 的解集是 $\text{[math]}$ ，那么 $\text{[math]}$ 的值是.

答案解析收藏纠错 + 选题
14. (2019九上·郑州月考) 如图①，在正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，点 $\text{[math]}$ 是对角线 $\text{[math]}$ 上一动点，设 $\text{[math]}$ 的长度为 $\text{[math]}$ 与 $\text{[math]}$ 的长度和为 $\text{[math]}$ ，图②是 $\text{[math]}$ 关于 $\text{[math]}$ 的函数图象，则图象上最低点 $\text{[math]}$ 的坐标为.

答案解析收藏纠错 + 选题
15. (2019·信阳模拟) 如图，四边形ABCD是菱形，AB=2，∠ABC=30°，点E是射线DA上一动点，把△CDE沿CE折叠，其中点D的对应点为点D′，若CD′垂直于菱形ABCD的边时，则DE的长为.

答案解析收藏纠错 + 选题

三、解答题三、解答题

16. (2023八上·西岗期末) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ .

答案解析收藏纠错 + 选题

17. (2019·信阳模拟) 雾霾天气严重影响市民的生活质量。在今年寒假期间，某校九年级一班的综合实践小组学生对“雾霾天气的主要成因”随机调查了所在城市部分市民，并对调查结果进行了整理，绘制了下图所示的不完整的统计图表：

组别	雾霾天气的主要成因	百分比
A	工业污染	45%
B	汽车尾气排放	$\text{[math]}$
C	炉烟气排放	15%
D	其他（滥砍滥伐等）	$\text{[math]}$

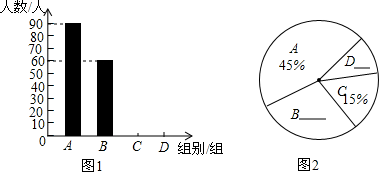
请根据统计图表回答下列问题：

（1）本次被调查的市民共有多少人？并求 $\text{[math]}$ 和 $\text{[math]}$ 的值；
（2）请补全条形统计图，并计算扇形统计图中扇形区域 $\text{[math]}$ 所对应的圆心角的度数；
（3）若该市有100万人口，请估计市民认为“工业污染和汽车尾气排放是雾霾天气主要成因”的人数.

答案解析收藏纠错 + 选题

18. (2019·信阳模拟) 如图，在平面直角坐标系 $\text{[math]}$ 中，一次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ，与反比例函数 $\text{[math]}$ 的图象交于 $\text{[math]}$ .
1. （1）求一次函数和反比例函数的表达式；
2. （2）设 $\text{[math]}$ 是直线 $\text{[math]}$ 上一点，过 $\text{[math]}$ 作 $\text{[math]}$ 轴，交反比例函数 $\text{[math]}$ 的图象于点 $\text{[math]}$ ，若 $\text{[math]}$ 为顶点的四边形为平行四边形，求点 $\text{[math]}$ 的坐标.
答案解析收藏纠错 + 选题
19. (2021九上·巩义期末) 如图，△ABC是⊙O的内接三角形，AB是⊙O的直径，OF⊥AB，交AC于点F，点E在AB的延长线上，射线EM经过点C，且∠ACE+∠AFO=180°.
1. （1）求证：EM是⊙O的切线；
2. （2）若∠A=∠E，BC= $\text{[math]}$ ，求阴影部分的面积.（结果保留 $\text{[math]}$ 和根号）.
答案解析收藏纠错 + 选题
20. (2019·信阳模拟) 茗阳阁位于河南省信阳市狮河区茶韵路一号，建成于2007年4月29日.是一栋由多种中国建筑元素，由雕栏飞檐、勾心斗角、斗拱图腾等多种形式的中国古代建筑元素汇聚而成，具有浓郁地方古建筑特色的塔式阁楼.茗阳阁是信阳新建的城市文化与形象的代表建筑之一，同时茗阳阁旁的风景也是优美至极.某数学课外兴趣小组为了测量建在山丘 $\text{[math]}$ 上的茗阳阁 $\text{[math]}$ 的高度，在山脚下的广场上 $\text{[math]}$ 处测得建筑物点 $\text{[math]}$ （即山顶）的仰角为20°，沿水平方向前进20米到达 $\text{[math]}$ 点，测得建筑物顶部 $\text{[math]}$ 点的仰角为45°，已知山丘 $\text{[math]}$ 高37.69米.求塔的高度 $\text{[math]}$ .（结果精确到1米，参考数据： $\text{[math]}$ ）

答案解析收藏纠错 + 选题
21. (2019·信阳模拟) 每年的6月5日为世界环保日，为了提倡低碳环保，某公司决定购买10台节省能源的新设备，现有甲、乙两种型号的设备可供选购，经调查：购买了3台甲型设备比购买2台乙型设备多花了16万元，购买2台甲型设备比购买3台乙型设备少花6万元.
1. （1）求甲、乙两种型号设备的价格；
2. （2）该公司经预算决定购买节省能源的新设备的资金不超过110万元，你认为该公司有几种购买方案；
3. （3）在（2）的条件下，已知甲型设备的产量为240吨/月，乙型设备的产量为180吨/月，若每月要求总产量不低于2040吨，为了节约资金，请你为该公司设计一种最省钱的购买方案.
答案解析收藏纠错 + 选题
22. (2019·信阳模拟) 如图（1），已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F.
1. （1）证明与推断：
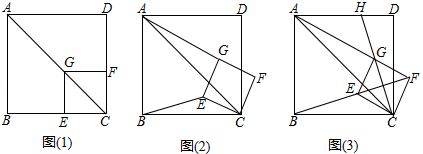
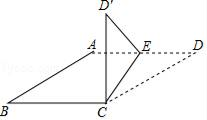
  ①求证：四边形CEGF是正方形；
  
  ②推断： $\text{[math]}$ 的值。
2. （2）探究与证明：
  将正方形CEGF绕点C顺时针方向旋转α角（0°＜α＜45°），如图（2）所示，试探究线段AG与BE之间的数量关系，并说明理由：
3. （3）拓展与运用：
  正方形CEGF在旋转过程中，当B，E，F三点在一条直线上时，如图（3）所示，延长CG交AD于点H.若AG=6，GH=2 $\text{[math]}$ ，则BC=.
答案解析收藏纠错 + 选题
23. (2019·信阳模拟) 如图所示，已知抛物线y=ax²+bx+c（a≠0）经过点A（﹣2，0）、B（4，0）、C（0，﹣8），与直线y=x﹣4交于B，D两点
1. （1）求抛物线的解析式并直接写出D点的坐标；
2. （2）点P为直线BD下方抛物线上的一个动点，试求出△BDP面积的最大值及此时点P的坐标；
3. （3）点Q是线段BD上异于B、D的动点，过点Q作QF⊥x轴于点F，交抛物线于点G，当△QDG为直角三角形时，直接写出点Q的坐标.
答案解析收藏纠错 + 选题