江苏省徐州市第26中学2016-2017学年八年级下学期期末...

更新时间：2017-08-25 浏览次数：1201 类型：期末考试

一、选择题

1. (2024八下·洪泽期中) 下列调查中，适合普查的是（）

A . 一批手机电池的使用寿命 B . 中国公民保护环境的意识 C . 你所在学校的男、女同学的人数 D . 端午节期间苏州市场上粽子的质量

答案解析收藏纠错 + 选题
2. (2017八下·徐州期末) 使分式 $\text{[math]}$ 有意义，则x的取值范围是（）

A . x≠1 B . x=1 C . x≤1 D . x≥1

答案解析收藏纠错 + 选题
3. (2017八下·徐州期末) 若正方形的面积是12cm² ，则边长a满足（）

A . 2cm＜a＜3cm B . 3cm＜a＜4cm C . 4cm＜a＜5cm D . 5cm＜a＜6cm

答案解析收藏纠错 + 选题
4. (2017八下·徐州期末) 若A（1，y₁），B（2，y₂）两点都在反比例函数y= $\text{[math]}$ 的图象上，则y₁与y₂的大小关系是（）

A . y₁＜y₂ B . y₁=y₂ C . y₁＞y₂ D . 无法确定

答案解析收藏纠错 + 选题
5. (2017八下·徐州期末) 已知▱ABCD中，AC、BD交于点O．下列结论中，不一定成立的是（）

A . ▱ABCD关于点O对称 B . OA=OC C . AC=BD D . ∠B=∠D

答案解析收藏纠错 + 选题
6. (2024八下·苏州月考) 一个不透明的袋子中装有2个红球、3个白球，每个球除颜色外都相同．从中任意摸出3个球，下列事件为必然事件的是（）

A . 至少有1个球是红球 B . 至少有1个球是白球 C . 至少有2个球是红球 D . 至少有2个球是白球

答案解析收藏纠错 + 选题
7. (2017八下·徐州期末)
如图，P为正方形ABCD的对角线BD上任一点，过点P作PE⊥BC于点E，PF⊥CD于点F，连接EF．给出以下4个结论：①△FPD是等腰直角三角形；②AP=EF；③AD=PD；④∠PFE=∠BAP．其中，所有正确的结论是（）

A . ①② B . ①④ C . ①②④ D . ①③④

答案解析收藏纠错 + 选题
8. (2017八下·徐州期末)
如图，已知在正方形网格中的两个格点三角形是位似形，它们的位似中心是（）

A . 点A B . 点B C . 点C D . 点D

答案解析收藏纠错 + 选题
9. (2017八下·徐州期末)
将矩形OABC如图放置，O为原点．若点A（﹣1，2），点B的纵坐标是 $\text{[math]}$ ，则点C的坐标是（）

A . （4，2） B . （2，4） C . （ $\text{[math]}$ ，3） D . （3， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
10. (2019·秀英模拟)
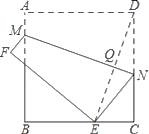
如图，正方形纸片ABCD的边长为4cm，点M、N分别在边AB、CD上．将该纸片沿MN折叠，使点D落在边BC上，落点为E，MN与DE相交于点Q．随着点M的移动，点Q移动路线长度的最大值是（）

A . 4cm B . 2cm C . $\text{[math]}$ cm D . 1cm

答案解析收藏纠错 + 选题

二、填空题

11. (2018八上·北京期中) 若分式 $\text{[math]}$ 的值为零，则x=．

答案解析收藏纠错 + 选题
12. (2017八下·徐州期末) 计算 $\text{[math]}$ ﹣ $\text{[math]}$ 的结果是．

答案解析收藏纠错 + 选题
13. (2017八下·徐州期末) 已知反比例函数的图象经过点（m，2）和（﹣2，3），则m的值为．

答案解析收藏纠错 + 选题
14. (2017八下·徐州期末) 若点P是线段AB的黄金分割点（PA＞PB），且AB=10cm，则PA≈cm．（精确到0.01cm）

答案解析收藏纠错 + 选题
15. (2017八下·徐州期末) 已知等式 $\text{[math]}$ ，对任意正整数n都成立．计算： $\text{[math]}$ =．

答案解析收藏纠错 + 选题
16. (2017八下·徐州期末)
如图，矩形OABC的顶点A、C的坐标分别为（4，0）、（0，2），对角线的交点为P，反比例函数y= $\text{[math]}$ （k＞0）的图象经过点P，与边BA、BC分别交于点D、E，连接OD、OE、DE，则△ODE的面积为．

答案解析收藏纠错 + 选题
17. (2020八下·溧阳期末)
如图，点A在函数y= $\text{[math]}$ （x＞0）的图象上，点B在函数y= $\text{[math]}$ （x＞0）的图象上，点C在x轴上．若AB∥x轴，则△ABC的面积为．

答案解析收藏纠错 + 选题
18. (2017八下·徐州期末) 已知菱形ABCD中，AC=6cm，BD=4cm．若以BD为边作正方形BDEF，则AF=cm．

答案解析收藏纠错 + 选题

三、解答题

19. (2017八下·徐州期末) 计算：（ $\text{[math]}$ + $\text{[math]}$ × $\text{[math]}$ ）× $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2017八下·徐州期末) 解分式方程： $\text{[math]}$ = $\text{[math]}$ ．

答案解析收藏纠错 + 选题
21. (2021八下·南京期末) 先化简[ $\text{[math]}$ ﹣ $\text{[math]}$ ]÷ $\text{[math]}$ ，然后从﹣1，0，1，2中选取一个你认为合适的数作为x的值代入求值．

答案解析收藏纠错 + 选题
22. (2020七下·麻城期末)
某校开展学生安全知识竞赛．现抽取部分学生的竞赛成绩（满分为100分，得分均为整数）进行统计，绘制了图中两幅不完整的统计图．根据图中信息，回答下列问题：
1. （1） a=，n=；
2. （2）补全频数分布直方图；
3. （3）该校共有2000名学生．若成绩在80分以上的为优秀，请你估计该校成绩优秀的学生人数．
答案解析收藏纠错 + 选题
23. (2017八下·徐州期末) 一个不透明的袋子中装有2个白球，1个红球，1个黑球，每个球除颜色外都相同，将球搅匀．
1. （1）从中任意摸出1个球，恰好摸到白球的概率是；
2. （2）先从中任意摸出1个球，再从余下的3个球中任意摸出1个球，求两次都摸到白球的概率．（用树状图或列表法求解）．
答案解析收藏纠错 + 选题
24. (2017八下·徐州期末)
如图，在▱ABCD中，∠BAD的平分线交BC于点E，∠ABC的平分线交AD于点F．
1. （1）求证：四边形ABEF是菱形；
2. （2）若AB=5，BF=8，AD= $\text{[math]}$ ，则▱ABCD的面积是．
答案解析收藏纠错 + 选题
25. (2017八下·徐州期末) “五一”期间，某商铺经营某种旅游纪念品．该商铺第一次批发购进该纪念品共花费3 000元，很快全部售完．接着，该商铺第二次批发购进该纪念品共花费9000元．已知第二次所购进该纪念品的数量是第一次的2倍还多300个，第二次的进价比第一次的进价提高了20%．
1. （1）求第一次购进该纪念品的进价是多少元？
2. （2）若该纪念品的两次售价均为9元/个，两次所购纪念品全部售完后，求该商铺两次共盈利多少元？
答案解析收藏纠错 + 选题
26. (2017八下·徐州期末)
如图，在平面直角坐标系中，点B是反比例函数y= $\text{[math]}$ 的图象上任意一点，将点B绕原点O顺时针方向旋转90°到点A．
1. （1）若点A的坐标为（4，2）．
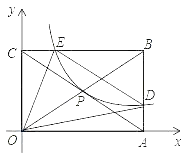
  ①求k的值；
  ②在反比例函数y= $\text{[math]}$ 的图象上是否存在一点P，使得△AOP是等腰三角形且∠AOP是顶角，若存在，写出点P的坐标；若不存在，请说明理由．
2. （2）当k=﹣1，点B在反比例函数y= $\text{[math]}$ 的图象上运动时，判断点A在怎样的图象上运动？并写出表达式．
答案解析收藏纠错 + 选题
27. (2017八下·徐州期末)
如图，已知直线a∥b，a、b之间的距离为4cm．A、B是直线a上的两个定点，C、D是直线b上的两个动点（点C在点D的左侧），且AB=CD=10cm，连接AC、BD、BC，将△ABC沿BC翻折得△A₁BC．
1. （1）当A₁、D两点重合时，AC=cm；
2. （2）当A₁、D两点不重合时，
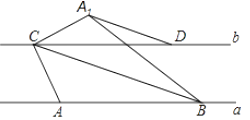
  ①连接A₁D，求证：A₁D∥BC；
  ②若以点A₁、C、B、D为顶点的四边形是矩形，求AC的长．
答案解析收藏纠错 + 选题