一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个备选项中,只有一项是符合题目要求的
-
-
2.
“

”是“

”的( )
A . 充要条件
B . 充分不必要条件
C . 必要不充分条件
D . 既不充分也不必要条件
-
3.
函数

的定义域是( )
-
4.
重庆市2013年各月的平均气温(℃)数据的茎叶图如下
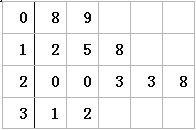
则这组数据中的中位数是( )
A . 19
B . 20
C . 21.5
D . 23
-
5.
某几何体的三视图如图所示,则该几何体的体积为( )
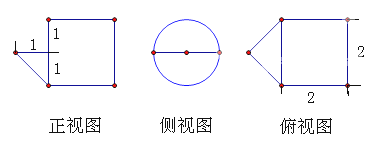
-
-
-
8.
执行如图(8)所示的程序框图,则输出s的值为( )
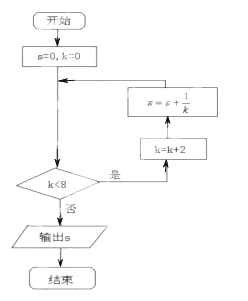
-
9.
设双曲线

的右焦点是F,左、右顶点分别是

过F做

的垂线与双曲线交于B,C两点,若,则双曲线的渐近线的斜率为( )
-
10.
若不等式组

, 表示的平面区域为三角形,且其面积等于

, 则m的值为( )
二、填空题:本大题共5小题,每小题5分,共25分,把答案写在答题卡相应的位置
-
11.
复数

的实部为
.
-
12.
若点

在以坐标原点为圆心的圆上,则该圆在点P处的切线方程为
.
-
13.
设

的内角A,B,C的对边分别为a,b,c,且

,

,

, 则c=
-
14.
设

, 则

的最大值为
.
-
15.
在区间

上随机地选择一个数p,则方程

有两个负根的概率为
.
三、解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤
-
16.
已知等差数列

满足

=2,前3项和

=

, 问:(1)求

的通项公式(2)设等比数列

满足

=

,

=

, 求

前n项和

.
-
(1)
求

的通项公式
-
-
17.
随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号t | 1 | 2 | 3 | 4 | 5 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
-
(1)
求y关于t的回归方程

-
(2)
用所求回归方程预测该地区2015年( )的人民币储蓄存款.
)的人民币储蓄存款.
附:回归方程 中
中
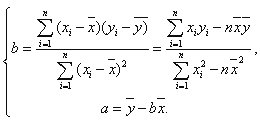
-
18.
已知函数

:(1)求

的最小周期和最小值;(2)将函数

的图像上每一点的横坐标伸长到原谅的两倍,纵坐标不变,得到函数

的图像。当 x ∈

, π 时,求

的值域。
-
(1)
求

的最小周期和最小值;
-
(2)
将函数

的图像上每一点的横坐标伸长到原谅的两倍,纵坐标不变,得到函数

的图像。当

时,求

的值域。
-
19.
已知函数

在

处取得极值,问(1)确定 α 的值;(2)若

=


,讨论的单调性。
-
(1)
确定

的值;
-
(2)
若

, 讨论的单调性。
-
20.
如题(20)图,三棱锥

中,平面

平面

,

, 点D、E在线段

上,且

,

点

在线段

上,且

-
(1)
证明:

平面

.
-
(2)
若四棱锥P-DFBC的体积为7,求线段BC的长。
-
21.
如图,椭圆

的左右焦点分别为

且过

的直线交椭圆于

两点,且

。
-
(1)
若

求椭圆的标准方程。
-
(2)
若

, 且

, 试确定椭圆离心率的取值范围。