一、选择题(本部分共12小题,每小题3分,共36分)
-
A . -2
B . -  C .
C .  D . 1
D . 1
-
-
-
-
A . x>0
B . x<0
C . x≠0的一切实数
D . x取任意实数
-
-
A . 菱形
B . 矩形
C . 正方形
D . 以上都不对
-
8.
(2024九下·南山开学考)
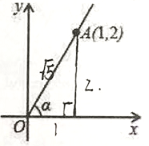
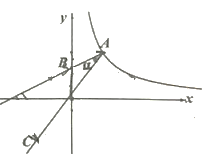
如图,在平面直角坐标系中,∠α的一边与x轴正半轴重合,顶点为坐标原点,另一边过点A(1,2),那么sinα的值为( )
-
9.
(2020九上·龙岗期末)
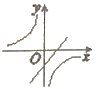
一次函数y=ax+a(a为常数,a≠0)与反比例函数y=

(a为常数,a≠0)在同一平面直角坐标系内的图像大致为( )
-
A . a≥-2
B . a≠2
C . a>-2且a≠2
D . a≥-2且a≠2
-
11.
(2020九上·龙岗期末)
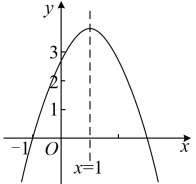
如图,二次函数y=ax
2+bx+c的图象与x轴交于点(-1,0),对称轴为直线x=1,2<c<3,下列结论:①abc>0;②9a+3b+c=0;③若点M(

,y
1),点N(

,y
2)是此函数图象上的两点,则y
1= y
2;④-1<a<

.其中正确的个数( )
A . 1个
B . 2个
C . 3个
D . 4个
-
12.
(2020九上·龙岗期末)
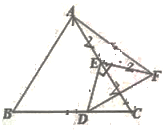
如图,△ABC是等边三角形,AB=4,E是AC的中点,D是直线BC上一动点,线段ED绕点E逆时针旋转90°,得到线段EF,当点D运动时,则AF的最小值为( )
二、填空题(本部分共4小题,每小题3分,共12分,)
-
-
-
-
16.
(2020九上·龙岗期末)
如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=

的图像上,作射线AB,再将射线AB绕点A按逆时针方向旋转α度,tanα=

,交反比例函数图象于点C,则点C的坐标为:
。
三、解答题(本大题共7题。其中17题5分,18题6分,19题7分,20题7分,21题8分,22题9分,23题10分,共52分)
-
-
-
19.
(2020九上·龙岗期末)
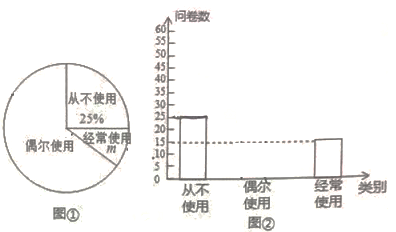
“低碳生活,绿色出行”是我们倡导的一种生活方式,某校为了解学生对共享单车的使用情况,随机抽取部分学生进行问卷调查,并将这次调查的结果绘制了以下两幅不完整的统计图。
根据所给信息,解答下列问题:
-
-
-
-
(4)
已知全校共3000名学生,请估计“经常使用”共享单车的学生大约有多少名?
-
20.
(2023九上·凤翔期末)
某超市经销一种成本为40元/kg的水产品,市场调查发现,按50元/kg销售,一个月能售出500kg,销售单位每涨0.1元,月销售量就减少1kg,针对这种水产品的销售情况,超市在月成本不超过10000元的情况下,使得月销售利润达到8000元,请你帮忙算算,销售单价定为多少?
-
21.
(2020九上·龙岗期末)
如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数y=

(m≠0)的图象的两个交点。

-
-
(2)
根据图象写出使一次函数的函数值小于反比例函数的函数值的x的取值范围。
-
22.
(2020九上·龙岗期末)
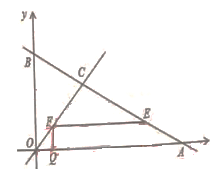
如图,直线y=

x+4与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动。分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外)。
-
-
-
23.
(2020九上·龙岗期末)
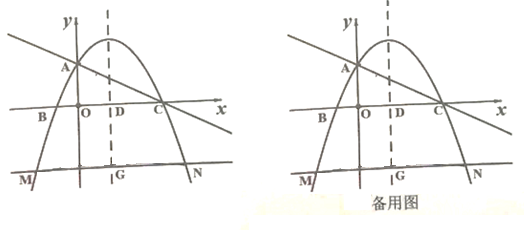
如图,在平面直角坐标系中,抛物线y=

x
2+bx+c与x轴交于B,C两点,与y轴交于点A,直线y=

x+2经过A,C两点,抛物线的对称轴与x轴交于点D,直线MN与对称轴交于点G,与抛物线交于M,N两点(点N在对称轴右侧),且MN∥x轴,MN=7。
-
-
-
(3)
过点A的直线与抛物线交于点F,当tan∠FAC=

时,求点F的坐标;
-
(4)
过点D作直线AC的垂线,交AC于点H,交y输于点K,连接CN,△AHK沿射线AC以每秒1个单位长度的速度移动,移动过程中△AHK与四边形DGNC产生重叠,设重叠面积为S,移动时间为t(0≤t≤

),请直接写出S与t的函数关系式。
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 

 B .
B . 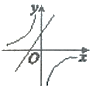 C .
C . 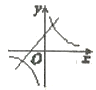 D .
D .