山西省吕梁市交城县2018-2019学年八年级下学期数学期中...

更新时间：2024-07-13 浏览次数：267 类型：期中考试

一、单选题

1. (2019八下·交城期中) 若二次根式 $\text{[math]}$ 有意义，则的取值范围是（）

A . x＞2 B . x＜2 C . x≥2 D . x≤2

答案解析收藏纠错 + 选题
2. (2023八下·长寿月考) 已知 $\text{[math]}$ ABCD中，∠A+∠C=200°，则∠B的度数是（）

A . 100° B . 160° C . 80° D . 60°

答案解析收藏纠错 + 选题
3. (2019八下·交城期中) 下列计算正确是 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2019八下·交城期中) 下列各组数中，以它们为边长的线段不能构成直角三角形的是（）

A . 1，，2 B . 1，2， C . 5，12，13 D . 1，，

答案解析收藏纠错 + 选题
5. (2019八下·交城期中) 如图，在▱ABCD中，CE⊥AB，垂足为点E，若∠A=130°，则∠BCE等于（）

A . 30° B . 40° C . 50° D . 45°

答案解析收藏纠错 + 选题
6. (2023八下·樟树期中) 已知四边形ABCD是平行四边形，对角线AC、BD交于点O，E是BC的中点，以下说法错误的是（）

A . OE= $\text{[math]}$ DC B . OA=OC C . ∠BOE=∠OBA D . ∠OBE=∠OCE

答案解析收藏纠错 + 选题
7. (2019八下·交城期中) 3世纪我国汉代的数学家赵爽在注解一部数学著作时，创作了一幅“弦图”，叫做“赵爽弦图”，并用数形结合的方法，给出了勾股定理的详细证明.这部中国古代数学著作是（）

A . 《周髀算经》 B . 《九章算术》 C . 《孙子算经》 D . 《海岛算经》

答案解析收藏纠错 + 选题
8. (2023九上·福田期中) 下列命题中，真命题是（　　）

A . 有两边相等的平行四边形是菱形 B . 有一个角是直角的四边形是矩形 C . 四个角相等的菱形是正方形 D . 两条对角线互相垂直且相等的四边形是正方形

答案解析收藏纠错 + 选题
9. (2020八下·固始期中) 如图，AB=BC=CD=DE=1，AB⊥BC，AC⊥CD，AD⊥DE，则AE=（）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
10. (2019八下·交城期中) 如图，将长方形ABCD沿直线EF折叠，使顶点C恰好落在顶点A处，已知AB＝4cm，AD＝8cm，则折痕EF的长为（）

A . 5cm B . $\text{[math]}$ cm C . $\text{[math]}$ cm D . $\text{[math]}$ cm

答案解析收藏纠错 + 选题

二、填空题

11. (2019八下·交城期中) 计算： $\text{[math]}$ =．

答案解析收藏纠错 + 选题
12. (2020八下·海东期末) 如图，平行四边形ABCD的对角线AC，BD相交于点O，请你添加一个适当的条件使其成为菱形（只填一个即可）．

答案解析收藏纠错 + 选题
13. (2019八下·交城期中) 如图，在Rt△ABC中，∠BAC=90°，AB=3，AC=4，AD⊥BC于点D，则AD的长为.

答案解析收藏纠错 + 选题
14. (2019八下·交城期中) 如图，AB是池塘两端，设计一方案测量AB的距离，首先取一点C，连接AC，BC，再取它们的中点D，E，测得DE=15米，则AB=米.

答案解析收藏纠错 + 选题
15. (2019八下·交城期中) 如图，在菱形ABCD中，对角线AC=6，AB=5，则菱形ABCD的面积为.

答案解析收藏纠错 + 选题
16. (2019八下·交城期中) 计算： $\text{[math]}$ = .

答案解析收藏纠错 + 选题
17. (2022八下·道县月考)
如图，△ABC中，CD⊥AB于D，E是AC的中点．若AD=6，DE=5，则CD的长等于

答案解析收藏纠错 + 选题
18. (2019八下·交城期中) 如图，在正方形ABCD中，O是对角线AC，BD的交点，过点O作OE⊥OF，分别交AB，BC于点E，F，若AE=4，CF=3，则四边形OEBF的面积为.

答案解析收藏纠错 + 选题

三、解答题

19. (2019八下·交城期中) 计算：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
20. (2019八下·交城期中) 如图都是由边长为1的小正方形组成的网格图，小正方形的顶点称为格点.请按下列要求作图.
1. （1）在图1中，已知线段AB，再作一条端点在格点上的线段CD= $\text{[math]}$ ，并且使CD⊥AB；
2. （2）在图2中，已知线段AB，以线段AB为边作一个格点菱形ABCD；
3. （3）在图3中，作一幅“赵爽弦图”.
答案解析收藏纠错 + 选题
21. (2019八下·交城期中) 如图，已知D是△ABC的边AB上一点，CE∥AB，DE交AC于点O，且OA=OC，猜想线段CD与线段AE的大小关系和位置关系，并加以证明.

答案解析收藏纠错 + 选题
22. (2019八下·交城期中) 阅读材料，并完成相应任务.
2000多年来，人们对勾股定理的证明颇感兴趣，不但因为这个定理重要、基本，还因为这个定理贴近人们的生活实际，所以很多人都探讨、研究它的证明，新的证法不断出现.

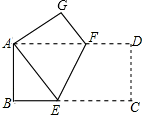
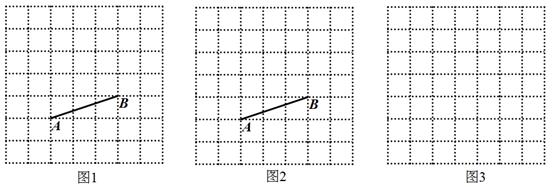
下面的图形是传说中毕达哥拉斯的证明图形：
1. （1）证明：①在图1中，∵ $\text{[math]}$
  
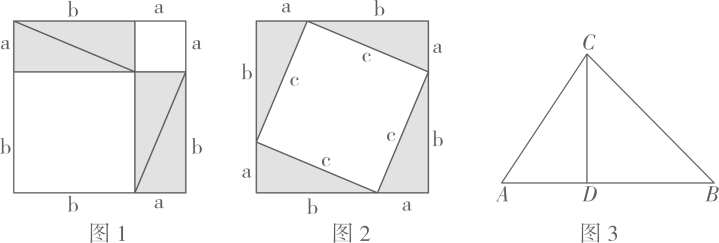
  $\text{[math]}$ 4个直角三角形的面积+两个正方形的面积
  
  =4×++ .
  
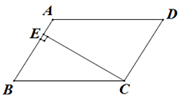
  ②在图2中，∵ $\text{[math]}$
  
  $\text{[math]}$ 4个直角三角形的面积+正方形的面积
  
  =4×+.
  
  ∴4× + + =4×+ .
  
  整理得： $\text{[math]}$
  
  ∴ .
  
  任务：将材料中的空缺部分补充完整；
2. （2）如图3，在△ABC中，∠A=60°，∠ACB=75°，CD⊥AB，AC=4，求BC的长.
答案解析收藏纠错 + 选题
23. (2022八下·滨海期末)
1. （1）如图1，四边形ABCD是正方形，G是BC上的任意一点，DE⊥AG，BF⊥AG，垂足分别为点E，F.求证： $\text{[math]}$ ；
2. （2）在图1的基础上，若过点C作CH⊥DE，垂足为点H，连接AH，CF，如图2.求证：四边形AFCH为平行四边形.
答案解析收藏纠错 + 选题
24. (2019八下·交城期中) 实践与探究
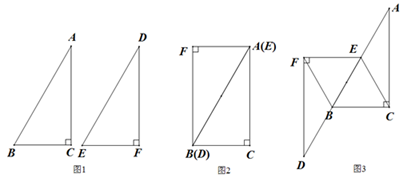
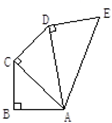
在综合实践课上，老师让同学们以两个全等的三角形纸片为操作对象，进行相关问题的探究.如图1，△ABC≌△DEF，其中∠ACB=90°，∠A=30°，AB=4.
1. （1）请直接写出EF=；
2. （2）新星小组将这两张纸片按如图2所示的方式放置后，经过观察发现四边形ACBF是矩形，请你证明这个结论.
3. （3）新星小组在图2的基础上，将△DEF纸片沿AB方向平移至如图3的位置，其中点E与AB的中点重合，连接CE，BF.请你判断四边形BCEF的形状，并证明你的结论.
答案解析收藏纠错 + 选题