湖北省孝感市2016-2017学年中考模拟数学考试试卷（五）

更新时间：2017-08-31 浏览次数：927 类型：中考模拟

一、选择题

1. (2017·孝感模拟) 中国人很早开始使用负数，中国古代数学著作《九章算术》的”方程“一章，在世界数学史上首次正式引入负数．如果收入1000元记作+1000元，那么﹣600元表示（）

A . 收入600元 B . 支出600元 C . 收入400元 D . 支出400元

答案解析收藏纠错 + 选题
2. (2017·孝感模拟) 如图，AB∥CD，射线AE交CD于点F，若∠1=105°，则∠2的度数是（）

A . 75° B . 85° C . 95° D . 105°

答案解析收藏纠错 + 选题
3. (2017·孝感模拟) 下列说法正确的是（）

A . 如果一件事不是必然发生的，那么它就不可能发生 B . 人有可能得病，也有可能不得病，因此得病与不得病的概率各占50% C . 某抽奖箱中有100张抽奖券，中奖概率是25%，首先甲抽取一张没中，接下来乙抽剩下的奖券，中奖的概率大于25% D . 某彩票的中奖机会是1%，买100张这种彩票一定是99张彩票不中奖，1张彩票中奖

答案解析收藏纠错 + 选题
4. (2017·孝感模拟) 如图是一个几何体的三视图（图中尺寸单位：cm），根据图中所示数据计算这个几何体的侧面积为（）cm² ．

A . 3π B . 6π C . 9π D . 12π

答案解析收藏纠错 + 选题
5. (2018·沧州模拟) 下列各式变形中，不正确的是（）

A . x⁴•x³=x⁷ B . $\text{[math]}$ =|x| C . （x²﹣ $\text{[math]}$ ）÷x=x﹣1 D . x²﹣x+1=（x﹣ $\text{[math]}$ ）²+ $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2017·孝感模拟) 如图，平行四边形ABCD的对角线AC、BD交于点O，E是AD的中点，连接BE交AC于点F，若S_△ABF=10，则S_△AEF（）

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
7. (2017·孝感模拟) 如图，过⊙O外一点P引⊙O的两条切线PA、PB，切点分别是A、B，OP交⊙O于点C，点D是 $\text{[math]}$ 上不与点A、点C重合的一个动点，连接AD、CD，若∠APB=60°，则∠ADC的度数是（）

A . 15 B . 20° C . 25° D . 30°

答案解析收藏纠错 + 选题
8. (2017·孝感模拟) 如图，将边长为10的正三角形OAB放置于平面直角坐标系xOy中，C是AB边上的动点（不与端点A、B重合），作CD⊥OB于点D，若点C，D都在双曲线y= $\text{[math]}$ 上（x＜0），则k的值为（）

A . ﹣9 B . ﹣9 $\text{[math]}$ C . ﹣18 $\text{[math]}$ D . ﹣25 $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2017·孝感模拟) 已知二次函数y=ax²+bx+c+2的图象如图所示，顶点为（﹣1，0），下列结论：①abc＜0；②b²﹣4ac=0；③a＞0；④4a﹣2b+c＞0．其中正确结论的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题

二、填空题

10. (2017·孝感模拟) 当x=时，分式 $\text{[math]}$ 的值为0．

答案解析收藏纠错 + 选题
11. (2021·肇源模拟) 分解因式：（p+1）（p﹣4）+3p=．

答案解析收藏纠错 + 选题
12. (2017·孝感模拟) 一组代数式：﹣ $\text{[math]}$ ， $\text{[math]}$ ，﹣ $\text{[math]}$ ， $\text{[math]}$ …，观察规律，则第10个代数式是．

答案解析收藏纠错 + 选题
13. (2017·孝感模拟) “赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形．有一“赵爽弦图”飞镖板，其直角三角形的两条直角边的长分别是2和4．小明同学距飞镖板一定距离向飞镖板投掷飞镖（假设投掷的飞镖均扎在飞镖板上），则投掷一次飞镖扎在中间小正形区域（含边）的概率是．

答案解析收藏纠错 + 选题
14. (2017·孝感模拟) 如图，矩形OABC的边OA，OC分别在坐标轴上，OA=4，OC=8，把△ABC沿着AC折叠．点B落在点B′处，AB′交y轴于点D，则点D的坐标是．

答案解析收藏纠错 + 选题
15. (2017·孝感模拟)
如图所示，有一些点组成形如四边形的图形，每条“边”（包括顶点）有n（n＞1）个点，当n=2017时，这个图形总的点数S=．

答案解析收藏纠错 + 选题

三、解答题

16. (2017·孝感模拟) 计算：|﹣ $\text{[math]}$ |+ $\text{[math]}$ ×（ $\text{[math]}$ ）^﹣1﹣ $\text{[math]}$ × $\text{[math]}$ ﹣（π﹣1）⁰ ．

答案解析收藏纠错 + 选题
17. (2017·孝感模拟) 如图，将矩形纸片ABCD（AD＞AB）折叠，使点C刚好落在线段AD上，且折痕分别与边BC，AD相交，设折叠后点C，D的对应点分别为点G，H，折痕分别与边BC，AD相交于点E，F．
1. （1）判断四边形CEGF的形状，并证明你的结论；
2. （2）若AB=3，BC=9，求线段CE的取值范围．
答案解析收藏纠错 + 选题
18. (2017·孝感模拟) 如图，Rt△ABC中，∠C=90°．
1. （1）求作：△ABC的内切圆⊙O（不写作法，保留作图痕迹）
2. （2）若⊙O的半径为2，tan∠A= $\text{[math]}$ ，求AB的长．
答案解析收藏纠错 + 选题
19. (2017·孝感模拟) 孝感市因董永孝感动天而得名，我市为了弘扬孝文化，某班举办了孝文化知识大赛，其规则是：每位参赛选手回答100道选择题，答对一题得1分，不答或错答不得分、不扣分，赛后对全体参赛选手的答题情况进行了相关统计，整理并绘制成如下图表：
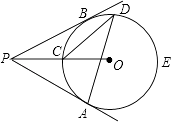
组别
分数段
频数（人）
频率
1
50≤x＜60
4
0.1
2
60≤x＜70
3
p
3
70≤x＜80
20
n
4
80≤x＜90
m
0.25
5
90≤x＜100
3
p
请根据以上图表信息，解答下列问题：
1. （1）表中m=，n=，p=；
2. （2）全体参赛选手成绩的中位数落在第组；
3. （3） ①若得分在80分以上（含80分）的选手可获奖，记者从所有参赛选手中随机采访1人，直接写出这名选手恰好是获奖者的概率．
  ②若该班班主任想从李明和王刚所在的成绩最差的第1组中选取两人进行家访，求恰好选中李明和王刚的概率．
答案解析收藏纠错 + 选题
20. (2017·孝感模拟) 关于x的方程x²﹣（2k﹣3）x+k²+1=0有两个不相等的实数根x₁、x₂ ．
1. （1）求k的取值范围；
2. （2）若x₁x₂+|x₁|+|x₂|=7，求k的值．
答案解析收藏纠错 + 选题
21. (2017·孝感模拟) 由于雾霾天气频发，市场上防护口罩出现热销，某医药公司每月固定生产甲、乙两种型号的防雾霾口罩共20万只，且所有产品当月全部售出，原料成本、销售单价及工人生产提成如表所示：
甲
乙
原料成本
12
8
销售单价
18
12
生产提成
1
0.6
1. （1）若该公司五月份的销售收入为330万元，求甲、乙两种型号的产品分别生产多少万只？
2. （2）公司实行计件工资制，即工人每生产一只口罩获得一定金额的提成，如果公司六月份投入总成本（原料总成本+生产提成总额）不超过216万元，应怎样安排甲、乙两种型号的产量，可使该月公司所获利润最大？并求出最大利润（利润=销售收入﹣投入总成本）
答案解析收藏纠错 + 选题
22. (2017·孝感模拟) 如图，AB为⊙O的直径，CD与⊙O相切与点D，AC⊥CD于C，并交⊙O于E，连接DE
1. （1）求证：AD平分∠CAB
2. （2）若CE=2，sin∠EAD= $\text{[math]}$ ，求⊙O的半径OA的长．
答案解析收藏纠错 + 选题
23. (2017·孝感模拟) 已知抛物线y=ax²﹣2ax+c与y轴交于C点，与x轴交于A、B两点，点A的坐标是（﹣1，0），O是坐标原点，且|OC|=3|OA|
1. （1）求抛物线的函数表达式和直线BC的函数表达式；
2. （2）
  如图1，D为y轴的负半轴上的一点，且OD=2，以OD为边作正方形ODEF，将正方形ODEF一每秒1个单位的速度沿x轴的正方形移动，在运动过程中，设正方形ODEF与△OBC重叠部分的面积为s，运动的时间为t秒（0＜t≤2）．在运动过程中，s是否存在最大值？如果存在，求出这个最大值；如果不存在，请说明理由．
3. （3）
  如图2，点P在直线BC下方的抛物线上，若∠PBC=∠ACO，求P点坐标．
答案解析收藏纠错 + 选题