
|
摸球的次数n |
100 |
200 |
300 |
500 |
800 |
1000 |
3000 |
|
摸到白球的次数m |
65 |
124 |
178 |
302 |
481 |
599 |
1803 |
|
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
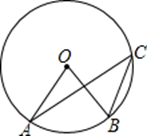
共有白球只.

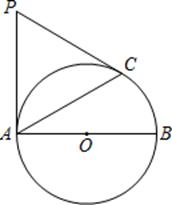
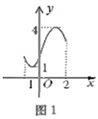
(示例)如图1,当 时;函数值y满足
,那么该段函数图象的横宽为2-(-1)=3,纵高为4-1=3.则
.
(应用)
①若m=1,是否存在这样的抛物线段,当 (
)时,函数值满足
若存在,请求出这段函数图象的k值;若不存在,请说明理由.
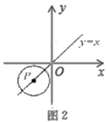
②如图2,若点P在直线y=x上运动,以点P为圆心, 为半径作圆,当AB段函数图象的k=1时,抛物线顶点恰好落在
上,请直接写出此时点P的坐标.