浙江省绍兴市上虞实验中学2020年数学中考模拟试卷（3月）

更新时间：2024-07-31 浏览次数：277 类型：中考模拟

一、单选题

1. (2024八下·岳阳楼期末) 若 $\text{[math]}$ = $\text{[math]}$ ，则 $\text{[math]}$ 的值为（　　）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020·绍兴模拟) 展览馆有 $\text{[math]}$ ， $\text{[math]}$ 两个入口， $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三个出口，则从 $\text{[math]}$ 入口进， $\text{[math]}$ 出口出的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2020·绍兴模拟)
某超市货架上摆放着某品牌红烧牛肉方便面，如图是它们的三视图，则货架上的红烧牛肉方便面至少有（）

A . 8 B . 9 C . 10 D . 11

答案解析收藏纠错 + 选题
4. (2024九上·茌平期末) 在平面直角坐标系xOy中，以点(－3，4)为圆心，4为半径的圆（）

A . 与x轴相交，与y轴相切 B . 与x轴相离，与y轴相交 C . 与x轴相切，与y轴相交 D . 与x轴相切，与y轴相离

答案解析收藏纠错 + 选题
5. (2022·江北模拟) sin70°，cos70°，tan70°的大小关系是（　　）

A . tan70°＜cos70°＜sin70° B . cos70°＜tan70°＜sin70° C . sin70°＜cos70°＜tan70° D . cos70°＜sin70°＜tan70°

答案解析收藏纠错 + 选题
6. (2020·绍兴模拟) 如图，AB是半圆O的直径，D，E是半圆上任意两点，连接AD，DE，AE与BD相交于点C，要使△ADC与△ABD相似，可以添加一个条件．下列添加的条件错误的是(　　)

A . ∠ACD＝∠DAB B . AD＝DE C . AD²＝BD·CD D . CD·AB＝AC·BD

答案解析收藏纠错 + 选题
7. (2020·绍兴模拟) 已知△ABC是正三角形，点D是边AC上一动点（不与A、C重合），以BD为边作正△BDE，边DE与边AB交于点F，则图中一定相似的三角形有（）对

A . 6 B . 5 C . 4 D . 3

答案解析收藏纠错 + 选题
8. (2020九上·芜湖期末)
如图，有一块边长为6cm的正三角形纸板，在它的三个角处分别截去一个彼此全等的筝形，再沿图中的虚线折起，做成一个无盖的直三棱柱纸盒，则该纸盒侧面积的最大值是（　　）

A . $\text{[math]}$ cm² B . $\text{[math]}$ cm² C . $\text{[math]}$ cm² D . $\text{[math]}$ cm²

答案解析收藏纠错 + 选题
9. (2020·绍兴模拟) 对于二次函数y=x²﹣2mx﹣3，有下列说法：
①它的图象与x轴有两个公共点；

②若当x≤1时y随x的增大而减小，则m=1；

③若将它的图象向左平移3个单位后过原点，则m=﹣1；

④若当x=4时的函数值与x=2时的函数值相等，则当x=6时的函数值为﹣3．

其中正确的说法是（　　）

A . ①②③ B . ①④ C . ②④ D . ①②④

答案解析收藏纠错 + 选题
10. (2020·绍兴模拟) 已知△ABC的两条中线的长分别为5、10，若第三条中线的长也是整数，则第三条中线长的最大值（）

A . 7 B . 8 C . 14 D . 15

答案解析收藏纠错 + 选题

二、填空题

11. 已知a=4，b=9，c是a，b的比例中项，则c=

答案解析收藏纠错 + 选题
12. (2020·绍兴模拟) 如图，在正方形网格中，小正方形的边长均为1，点A，B，C都是格点，则cos∠BAC=．

答案解析收藏纠错 + 选题
13. (2020·绍兴模拟) ⊙O的半径为1，弦AB= $\text{[math]}$ ，弦AC= $\text{[math]}$ ，则∠BAC度数为．

答案解析收藏纠错 + 选题
14. (2020·绍兴模拟)
如图，半径为1的半圆形纸片，按如图方式折叠，使对折后半圆弧的中点M与圆心O重合，则图中阴影部分的面积是．

答案解析收藏纠错 + 选题
15. (2020·绍兴模拟) $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，如果以点 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径，且 $\text{[math]}$ 与斜边 $\text{[math]}$ 仅有一个公共点，那么半径 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题
16. (2022九下·内江开学考) 如图，直角三角形ABC中，∠ACB=90°，AB=10，BC=6，在线段AB上取一点D，作DF⊥AB交AC于点F，现将△ADF沿DF折叠，使点A落在线段DB上，对应点记为A₁；AD的中点E的对应点记为E₁ ，若△E₁FA₁∽△E₁BF，则AD=．

答案解析收藏纠错 + 选题

三、解答题

17. (2020·绍兴模拟) 计算：如图，半径为3的⊙A经过原点O和点C(0，2)，B是y轴左侧⊙A优弧上一点，求tan∠OBC的值．

答案解析收藏纠错 + 选题
18. (2020·绍兴模拟) 已知二次函数y＝ax²＋bx＋c的图象过A(2，0)，B(0，－1)和C(4，5)三点，求二次函数的解析式．

答案解析收藏纠错 + 选题
19. (2023九上·安岳月考) 如图，小红同学用仪器测量一棵大树AB的高度，在C处测得∠ADG=30°，在E处测得∠AFG=60°，CE=8米，仪器高度CD=1.5米，求这棵树AB的高度（结果精确到0.1， $\text{[math]}$ ≈1.73）．

答案解析收藏纠错 + 选题
20. (2020·绍兴模拟) 一个口袋中放有20个球，其中红球6个，白球和黑球各若干个，每个球除了颜色外没有任何区别．小王通过大量反复试验（每次取一个球，放回搅匀后取第二个）发现，取得黑球的频率稳定在0.4左右．
1. （1）请你估计袋中黑球的个数；
2. （2）若小王取出的第一个球是白球，将它放在桌上，闭上眼睛从袋中余下的球中再任意一个球，取出红球的概率是多少？
答案解析收藏纠错 + 选题
21. (2020·绍兴模拟) 如图1，以△ABC的边AB为直径的⊙O交边BC于点E，过点E作⊙O的切线交AC于点D，且ED⊥AC．
1. （1）试判断△ABC的形状，并说明理由；
2. （2）如图2，若线段AB、DE的延长线交于点F，∠C=75°，CD= $\text{[math]}$ ，求⊙O的半径和BF的长
答案解析收藏纠错 + 选题
22. (2020·绍兴模拟) 阅读：我们约定，在平面直角坐标系中，经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线，叫该点的“特征线”．例如，点M（1，3）的特征线有：x=1，y=3，y=x+2，y=﹣x+4．问题与探究：如图，在平面直角坐标系中有正方形OABC，点B在第一象限，A、C分别在x轴和y轴上，抛物线 $\text{[math]}$ 经过B、C两点，顶点D在正方形内部．
1. （1）直接写出点D（m，n）所有的特征线；
2. （2）若点D有一条特征线是y=x+1，求此抛物线的解析式；
3. （3）点P是AB边上除点A外的任意一点，连接OP，将△OAP沿着OP折叠，点A落在点A′的位置，当点A′在平行于y轴的D点的特征线上时，满足（2）中条件的抛物线向下平移多少距离，其顶点落在OP上？
答案解析收藏纠错 + 选题
23. (2020·绍兴模拟)
1. （1）如图1，已知△ABC中AB=AC，∠BAC=36°，BD是角平分线，求证：点D是线段AC的黄金分割点；
2. （2）如图2，正五边形的边长为2，连结对角线AD、BE、CE，线段AD分别与BE和CE相交于点M、N，求MN的长；
3. （3）设⊙O的半径为r，直接写出它的内接正十边形的长=（用r的代数式表示）．
答案解析收藏纠错 + 选题
24. (2020·绍兴模拟) 在平面直角坐标系xOy中，一块含60°角的三角板作如图摆放，斜边AB在x轴上，直角顶点C在y轴正半轴上，已知点A（﹣1，0）．
1. （1）请直接写出点B、C的坐标：B（）、C（）；并求经过A、B、C三点的抛物线解析式；
2. （2）现有与上述三角板完全一样的三角板DEF（其中∠EDF=90°，∠DEF=60°），把顶点E放在线段AB上（点E是不与A、B两点重合的动点），并使ED所在直线经过点C．此时，EF所在直线与（1）中的抛物线交于点M．
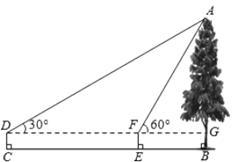
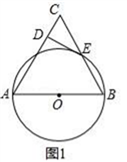
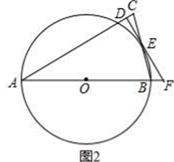
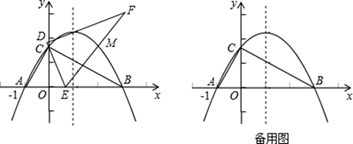
  ①设AE=x，当x为何值时，△OCE∽△OBC；
  
  ②在①的条件下探究：抛物线的对称轴上是否存在点P使△PEM是等腰三角形？若存在，请写出点P的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题