福建省龙岩市永定区、连城县2019年中考数学5月模拟考试试卷

更新时间：2024-07-13 浏览次数：248 类型：中考模拟

一、选择题（本题共10小题，每小题4分，共40分）

1. (2019·永定模拟) 下列实数为无理数的是（）

A . ﹣5 B . $\text{[math]}$ C . 0 D . π

答案解析收藏纠错 + 选题
2. (2019·永定模拟) 如图，这是由5个大小相同的正方体搭成的几何体，该几何体的左视图（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2019·永定模拟) 在平面直角坐标系中，点A（1， $\text{[math]}$ ）绕原点顺时针旋转90°，得到点A'，则点A'的坐标为（）

A . （﹣ $\text{[math]}$ ，1） B . （ $\text{[math]}$ ，﹣1） C . （﹣1， $\text{[math]}$ ） D . （1， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
4. (2020七上·兰山期中) 这段时间，一个叫“学习强国”的理论学习平台火了，很多人主动下载、积极打卡，兴起了一股全民学习的热潮．据不完全统计，截止4月2号，华为官方应用市场“学习强国APP”下载量已达8830万次，请将8830万用科学记数法表示为（）

A . 0.883×10⁹ B . 8.83×10⁸ C . 8.83×10⁷ D . 88.3×10⁶

答案解析收藏纠错 + 选题
5. (2019·永定模拟) 下列运算正确的是（）

A . 7a﹣a＝6 B . a²•a³＝a⁵ C . （a³）³＝a⁶ D . （ab）⁴＝ab⁴

答案解析收藏纠错 + 选题
6. (2019·永定模拟) 不等式组 $\text{[math]}$ 的解集在数轴上表示为（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2019·永定模拟) 为迎接中考体育加试，小刚和小亮分别统计了自己最近10次跳绳成绩，下列统计中能用来比较两人成绩稳定程度的是（）

A . 平均数 B . 中位数 C . 众数 D . 方差

答案解析收藏纠错 + 选题
8. (2019·永定模拟) 《九章算术》是我国古代第一部自成体系的数学专著，代表了东方数学的最高成就．它的算法体系至今仍在推动着计算机的发展和应用．书中记载：“今有圆材埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”译为：“今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯这木材，锯口深1寸（ED＝1寸），锯道长1尺（AB＝1尺＝10寸）”，问这块圆柱形木材的直径是多少？”
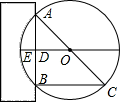
如图所示，请根据所学知识计算：圆柱形木材的直径AC是（）

A . 13寸 B . 20寸 C . 26寸 D . 28寸

答案解析收藏纠错 + 选题
9. (2019·永定模拟) 如图，平行于x轴的直线与函数y＝ $\text{[math]}$ （k₁＞0，x＞0），y＝ $\text{[math]}$ （k₂＞0，x＞0）的图象分别相交于A ， B两点，点A在点B的右侧，C为x轴上的一个动点，若△ABC的面积为4，则k₁﹣k₂的值为（）

A . 8 B . ﹣8 C . 4 D . ﹣4

答案解析收藏纠错 + 选题
10. (2019·永定模拟) 在△ABC中，若O为BC边的中点，则必有：AB²+AC²＝2AO²+2BO²成立.依据以上结论，解决如下问题：如图，在矩形DEFG中，已知DE＝4，EF＝3，点P在以DE为直径的半圆上运动，则PF²+PG²的最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 34 D . 10

答案解析收藏纠错 + 选题

二、填空题（本题共6小题，每小题4分，共24分）

11. (2019·永定模拟) 已知a是x²﹣3x+1＝0的根，则2a²﹣6a＝．

答案解析收藏纠错 + 选题
12. (2021九上·新抚期末) 圆锥的底面半径为3cm ，母线长为5cm ，则它的侧面积为．

答案解析收藏纠错 + 选题
13. (2021·福州模拟) 一个暗箱中放有除颜色外其他完全相同的n个红球，18个黄球，9个白球，现将球搅匀后，任意摸出1个球记下颜色，再放回暗箱，通过大量重复试验后发现，摸到黄球的频率稳定在30%附近，由此可以估算的n值是．

答案解析收藏纠错 + 选题
14. (2019·永定模拟) 如图，AB、AC都是圆O的弦，OM⊥AB ， ON⊥AC ，垂足分别为M、N ，如果MN＝3，那么BC＝．

答案解析收藏纠错 + 选题
15. (2019·永定模拟) 小卖部从批发市场购进一批李子，在销售了部分李子之后，余下的每千克降价3元，直至全部售完．销售金额（元）与李子销售量（千克）之间的关系如图所示．若销售这批李子一共赢利220元，那么这批李子的进价是元．

答案解析收藏纠错 + 选题
16. (2019·永定模拟) 如图，在矩形ABCD中，AB＝3，CB＝2，点E为线段AB上的动点，将△CBE沿CE折叠，使点B落在矩形内点F处，下列结论正确的是（写出所有符合题意结论的序号）
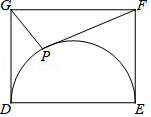
①当E为线段AB中点时，AF∥CE；

②当E为线段AB中点时，AF＝ $\text{[math]}$ ；

③当A、F、C三点共线时，AE＝ $\text{[math]}$ ；

④当A、F、C三点共线时，△CEF≌△AEF ．

答案解析收藏纠错 + 选题

三、解答题：（本题共9小题，共86分）

17. (2019·永定模拟) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2019·永定模拟) 先化简 $\text{[math]}$ ÷（ $\text{[math]}$ ﹣x+1），然后从﹣ $\text{[math]}$ ＜x＜ $\text{[math]}$ 的范围内选取一个合适的整数作为x的值代入求值．

答案解析收藏纠错 + 选题
19. (2019·永定模拟) 如图，已知∠MON ，点B ， C分别在射线OM ， ON上，且OB＝OC ．
1. （1）用直尺和圆规作出∠MON的角平分线OP ，在射线OP上取一点A ，分别连接AB、AC（只需保留作图痕迹，不要求写作法）．
2. （2）在（1）的条件下求证：AB＝AC ．
答案解析收藏纠错 + 选题
20. (2019·永定模拟) 某旅游团到永定土楼观光，计划购买A型、B型两种型号的土楼模型．若购买8个A型土楼模型和5个B型土楼模型需用1540元；若购买4个A型土楼模型和6个B型土楼模型需用1120元．求A ， B两种型号土楼模型的单价分别是多少元．

答案解析收藏纠错 + 选题
21. (2019·永定模拟) 根据最新公布的福建高考改革方案，从2021年开始我省高考将实行“3+1+2”模式．“3“指的是语文、数学、外语三科为必考科目，不分文理科，由全国统一命题；“1+2“为高中学业水平选择性考试，其中“1“为在物理、历史2科中选择1科；“2“为在思想政治、地理、化学、生物4科中选择2科．现对该校某班选科情况进行调查，对调查结果进行了分析统计，并制作了两幅不完整的统计图．

请根据以上信息，完成下列问题：
1. （1）该班共有学生人；
2. （2）请将条形统计图补充完整；
3. （3）该班某同学物理成绩特别优异，已经从物理、历史学科中选定物理，还需从余下思想政治、地理、化学、生物（分别记为A、B、C、D）4门科目中任意选择两门，请用列表或画树状图的方法，求出该同学恰好选中化学、生物两科的概率．
答案解析收藏纠错 + 选题
22. (2019·永定模拟) 如图，D为⊙O上一点，点C在直径BA的延长线上，∠CDA＝∠CBD ．
1. （1）求证：CD是⊙O的切线；
2. （2）过点B作⊙O的切线交CD的延长线于点E ，若BC＝4，tan∠ABD＝ $\text{[math]}$ ，求BE的长．
答案解析收藏纠错 + 选题
23. (2019·永定模拟) 知识背景：
当a＞0且x＞0时，因为 $\text{[math]}$ ，所以x﹣2 $\text{[math]}$ ≥0，

从而 $\text{[math]}$ （当 $\text{[math]}$ ＝ $\text{[math]}$ ，即x＝ $\text{[math]}$ 时取等号）．

设函数y＝x+ $\text{[math]}$ （x＞0，a＞0），由上述结论可知：当x＝ $\text{[math]}$ 时，该函数有最小值2 $\text{[math]}$ ．

应用举例

已知函数为y₁＝x（x＞0）与函数y₂＝ $\text{[math]}$ （x＞0），则当x＝ $\text{[math]}$ 时，y₁+y₂＝x+ $\text{[math]}$ 有最小值为2 $\text{[math]}$ ．

解决问题
1. （1）已知函数为y₁＝x﹣1（x＞1）与函数y₂＝（x﹣1）²+9（x＞1），当x取何值时， $\text{[math]}$ 有最小值？最小值是多少？
2. （2）已知某设备租赁使用成本包含以下三部分：一是设备的安装调试费用，共490元；二是设备的租赁使用费用，每天200元；三是设备的折旧费用，它与使用天数的平方成正比，比例系数为0.001．若设该设备的租赁使用天数为x天，则当x取何值时，该设备平均每天的租赁使用成本最低？最低是多少元？
答案解析收藏纠错 + 选题
24. (2019·永定模拟) 定义：点P是四边形ABCD内一点，若三角形△PAB ， △PBC ， △PCD ， △PDA均为等腰三角形，则称点P是四边形ABCD的一个“准中心”，如，正方形的中心就是它的一个“准中心”．
1. （1）如图，已知点P是正方形ABCD内的一点，且∠PBC＝∠PCB＝60°，证明点P是正四边形ABCD的一个“准中心”；
2. （2）填空：正方形ABCD共有个“准中心”；
3. （3）已知∠BAD＝60°，AB＝AD＝6，点C是∠BAD平分线上的动点，问在四边形ABCD的对角线AC上最多存在几个“准中心”点P（自行画出示意图），并求出每个“准中心”点P对应线段AC的长（精确到个位）．
答案解析收藏纠错 + 选题
25. (2019·永定模拟) 在平面直角坐标系中，点O（0，0），点A（1，0）．已知抛物线y＝x²+mx﹣2m（m是常数），顶点为P ．
（Ⅰ）当抛物线经过点A时，求顶点P的坐标；

（Ⅱ）若点P在x轴下方，当∠AOP＝45°时，若函数值y＞0，求对应自变量x的取值范围；

（Ⅲ）无论m取何值，该抛物线都经过定点H ．当∠AHP＝45°时，求抛物线的解析式．

答案解析收藏纠错 + 选题