 B .
B .  C .
C .  D .
D . 
根据以上作图过程及所作图形,下列结论中不正确是
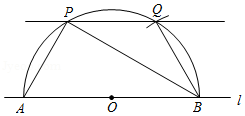
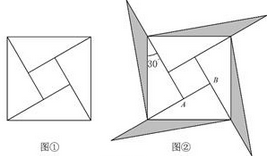
① ;②
;③
为等腰三角形;④
,
其中正确结论的序号为.
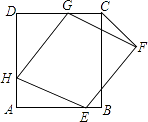
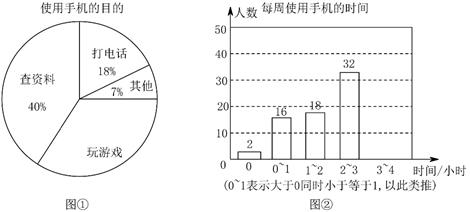
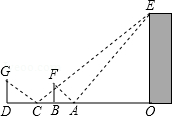
①当点 在
之间,以
为直径的圆与直线
相切,试求
的值;
②当直线 上恰好有2点是
,
两点的勾股点时,试求相应
的取值范围.
①若 ,求
的值;
②证明:无论 为何值,
恒为直角三角形.