河北省保定市定兴县2019年中考数学一模考试试卷

更新时间：2024-07-13 浏览次数：192 类型：中考模拟

一、选择题

1. (2019·定兴模拟) 下列图形中，线段MN的长度表示点M到直线l的距离的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2019·定兴模拟) 为你点赞，你是最棒的！下列四种QQ表情图片都可以用来为你点赞！其中是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2019·定兴模拟) 下列运算中，正确是（）

A . a²•a²＝2a² B . （a³）³＝a⁹ C . a﹣a²＝﹣a D . （ab）²＝ab²

答案解析收藏纠错 + 选题
4. (2019·定兴模拟) 数学课上，老师在黑板上写了四个式子，如图所示，其中计算结果为整数的是（）

A . ① B . ② C . ③ D . ④

答案解析收藏纠错 + 选题
5. (2019·安次模拟) 如图是由7个同样大小的正方体摆成的几何体．将正方体①移走后，所得几何体（）

A . 主视图改变，俯视图改变 B . 左视图改变，俯视图改变 C . 俯视图不变，左视图改变 D . 主视图不变，左视图不变

答案解析收藏纠错 + 选题
6. (2019·定兴模拟) 从河北省统计局获悉，2018年前三季度新能源发电量保持快速增长，其中垃圾焚烧发电量6.9亿千瓦时，同比增长59%，6.9亿用科学记数法表示为a×10ⁿ万，则n的值为（）

A . 9 B . 8 C . 5 D . 4

答案解析收藏纠错 + 选题
7. (2019·定兴模拟) 如图，给出线段a、h ，作等腰三角形ABC ，使AB＝AC＝a ， BC边上的高AD＝h ．张红的作法是：（1）作线段AD＝h；（2）作线段AD的垂线MN；（3）以点A为圆心，a为半径作弧，与MN分别交于点B、C；（4）连接AB、AC、△ABC为所求作的等腰三角形．上述作法的四个步骤中，你认为有不正确一步是（）

A . （1） B . （2） C . （3） D . （4）

答案解析收藏纠错 + 选题
8. (2019·定兴模拟) 下面是嘉嘉和琪琪的对话，根据对话内容，则x的值可能是
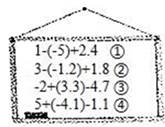
嘉嘉：我能正确化简分式（ $\text{[math]}$ ）÷ $\text{[math]}$

琪琪：我给x取一个值，使你化简分式后所得代数式的值大于0，你能猜出来我给x取的值是几吗？（）

A . ﹣1 B . 1 C . 0 D . 2

答案解析收藏纠错 + 选题
9. (2019·定兴模拟) 如图，将边长为5的正六边形ABCDEF沿直线MN折叠，则图中阴影部分周长为（）

A . 20 B . 24 C . 30 D . 35

答案解析收藏纠错 + 选题
10. (2019·定兴模拟) 某射击运动员练习射击，5次成绩分别是：8、9、7、8、x（单位：环）．下列说法中正确是（）

A . 若这5次成绩的中位数为8，则x＝8 B . 若这5次成绩的众数是8，则x＝8 C . 若这5次成绩的方差为8，则x＝8 D . 若这5次成绩的平均成绩是8，则x＝8

答案解析收藏纠错 + 选题
11. (2019·定兴模拟) 如图，△ABC是等边三角形，点P是三角形内的任意一点，PD∥AB ， PE∥BC ， PF∥AC ，若△ABC的周长为12，则PD+PE+PF＝（）

A . 12 B . 8 C . 4 D . 3

答案解析收藏纠错 + 选题
12. (2019·定兴模拟)
如图，要修建一条公路，从A村沿北偏东75°方向到B村，从B村沿北偏西25°方向到C村．若要保持公路CE与AB的方向一致，则∠ECB的度数为（）

A . 80° B . 90° C . 100° D . 105°

答案解析收藏纠错 + 选题
13. (2019·定兴模拟) 如图，将△ABC沿BC边上的中线AD平移到△A'B'C'的位置，已知△ABC的面积为9，阴影部分三角形的面积为4.若AA'＝1，则A'D等于（）

A . 2 B . 3 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
14. (2019·定兴模拟) 如图，小明为了测量河宽AB ，先在BA延长线上取一点D ，再在同岸取一点C ，测得∠CAD＝60°，∠BCA＝30°，AC＝15m ，那么河AB宽为（）

A . 15m B . $\text{[math]}$ m C . $\text{[math]}$ m D . $\text{[math]}$ m

答案解析收藏纠错 + 选题
15. (2019·定兴模拟) 如图，用四根长为5cm的铁丝，首尾相接围成一个正方形（接点不固定），要将它的四边按图中的方式向外等距离移动acm ，同时添加另外四根长为5cm的铁丝（虚线部分）得到一个新的正八边形，则a的值为（）

A . 4cm B . 5cm C . 5 $\text{[math]}$ cm D . $\text{[math]}$ cm

答案解析收藏纠错 + 选题
16. (2019·定兴模拟) 二次函数y＝x²+bx﹣1的图象如图，对称轴为直线x＝1，若关于x的一元二次方程x²﹣2x﹣1﹣t＝0（t为实数）在﹣1＜x＜4的范围内有实数解，则t的取值范围是（）

A . t≥﹣2 B . ﹣2≤t＜7 C . ﹣2≤t＜2 D . 2＜t＜7

答案解析收藏纠错 + 选题

二、填空题

17. (2024九下·天祝模拟) 计算： $\text{[math]}$ + $\text{[math]}$ =．

答案解析收藏纠错 + 选题
18. (2019·定兴模拟) 若m、n互为倒数，则mn²﹣（n﹣1）的值为．

答案解析收藏纠错 + 选题
19. (2019·定兴模拟) 如图，在△ABC中，BC＝AC＝5，AB＝8，CD为AB边的高，点A在x轴上，点B在y轴上，点C在第一象限，若A从原点出发，沿x轴向右以每秒1个单位长的速度运动，则点B随之沿y轴下滑，并带动△ABC在平面内滑动，设运动时间为t秒，当B到达原点时停止运动
1. （1）连接OC ，线段OC的长随t的变化而变化，当OC最大时，t＝；
2. （2）当△ABC的边与坐标轴平行时，t＝．
答案解析收藏纠错 + 选题

三、解答题

20. (2019·定兴模拟) 老师在黑板上写出如图所示的算式
1. （1）嘉嘉在“□”中填入﹣6，请帮他计算“◇”中填入的数字；
2. （2）淇淇说，“□”和“◇”填入的一定是两个不同的数，淇淇的说法对吗？请说明理由．
  $\text{[math]}$
答案解析收藏纠错 + 选题
21. (2019·定兴模拟) 小明对A ， B ， C ， D四个中小型超市的女工人数进行了统计，并绘制了下面的统计图表，已知A超市有女工20人．

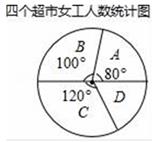
超市

A

B

C

D

女工人数占比

62.5%

62.5%

50%

75%
1. （1） A超市共有员工多少人？B超市有女工多少人？
2. （2）若从这些女工中随机选出一个，求正好是C超市的概率；
3. （3）现在D超市又招进男、女员工各1人，D超市女工占比还是75%吗？甲同学认为是，乙同学认为不是，你认为谁说的对，并说明理由．
答案解析收藏纠错 + 选题
22. (2019·定兴模拟) 探究：
在一次聚会上，规定每两个人见面必须握手，且只握手1次
1. （1）若参加聚会的人数为3，则共握手次：；若参加聚会的人数为5，则共握手次；
2. （2）若参加聚会的人数为n（n为正整数），则共握手次；
3. （3）若参加聚会的人共握手28次，请求出参加聚会的人数.
4. （4）拓展：
  嘉嘉给琪琪出题：
  
  “若线段AB上共有m个点（含端点A，B），线段总数为30，求m的值.”
  
  琪琪的思考：“在这个问题上，线段总数不可能为30”
  
  琪琪的思考对吗？为什么？
答案解析收藏纠错 + 选题
23. (2019·定兴模拟) 老师布置了一个作业，如下：
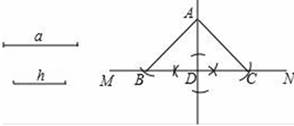
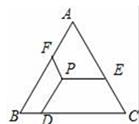
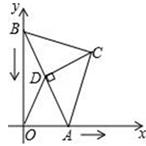
已知：如图1▱ABCD的对角线AC的垂直平分线EF交AD于点F ，交BC于点E ，交AC于点O

求证：四边形AECF是菱形．

某同学写出了如图2所示的证明过程，老师说该同学的作业是不正确，请你解答下列问题：
1. （1）能找出该同学不正确原因吗？请你指出来；
2. （2）请你给出本题的正确证明过程．
答案解析收藏纠错 + 选题
24. (2019·定兴模拟) 如图，在平面直角坐标系中，反比例函数y＝ $\text{[math]}$ （x＞0）的图象与边长是6的正方形OABC的两边AB ， BC分别相交于M ， N两点．
1. （1）若点M是AB边的中点，求反比例函数y＝ $\text{[math]}$ 的解析式和点N的坐标；
2. （2）若AM＝2，求直线MN的解析式及△OMN的面积．
答案解析收藏纠错 + 选题
25. (2019·定兴模拟) 如图1，四边形ABCD是正方形，且AB＝8，点O与B重合，以O为圆心，作半径长为5的半圆O ，交BC于点E ，交AB于点F ，交AB的延长线于点G ．
1. （1）发现：M是半圆O上任意一点，连接AM ，则AM的最大值为；
2. （2）思考：如图2，将半圆O绕点F逆时针旋转，记旋转角为α（0°＜α＜180°）
  当α＝90°时，求半圆O落在正方形内部的弧长；
3. （3）在旋转过程中，若半圆O与正方形ABCD的边相切时，请直接写出此时点A到切点的距离．（注：sin37°＝ $\text{[math]}$ ，sin53°＝ $\text{[math]}$ ，tan37°＝ $\text{[math]}$ ）
答案解析收藏纠错 + 选题
26. (2019·定兴模拟) 如图1，地面BD上两根等长立柱AB ， CD之间悬挂一根近似成抛物线y＝ $\text{[math]}$ x²﹣ $\text{[math]}$ x+3的绳子．
1. （1）求绳子最低点离地面的距离；
2. （2）因实际需要，在离AB为3米的位置处用一根立柱MN撑起绳子（如图2），使左边抛物线F₁的最低点距MN为1米，离地面1.8米，求MN的长；
3. （3）将立柱MN的长度提升为3米，通过调整MN的位置，使抛物线F₂对应函数的二次项系数始终为 $\text{[math]}$ ，设MN离AB的距离为m ，抛物线F₂的顶点离地面距离为k ，当2≤k≤2.5时，求m的取值范围．
答案解析收藏纠错 + 选题