浙江省杭州市2020年数学中考复习卷（一）

更新时间：2020-05-22 浏览次数：299 类型：中考模拟

一、选择题：本大题有10个小题，每小题3分，共30分．

1. (2020·杭州模拟) 若x²=4，则x=（）

A . -2 B . 2 C . -2或2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020·杭州模拟) 2019年“十·一”黄金周期间(7天)，某市旅游总收入约为101.7亿元．其中101.7亿用科学记数法表示为（）

A . 101.7×10⁶ B . 10.17×10⁹ C . 1.017×10¹⁰ D . 1.017×10⁸

答案解析收藏纠错 + 选题
3. (2020·杭州模拟) 下列计算错误的是（）

A . 2a²+3a²=5a⁴ B . (3ab³)²=9a²b⁶ C . (x²)³=x⁶ D . a·a²=a³

答案解析收藏纠错 + 选题
4. (2020·杭州模拟) 如图，AB是⊙O的直径，CD是⊙O的弦，若∠ACD=37°，则劣弧 $\text{[math]}$ 的度数为（）

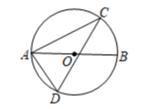
A . 74° B . 106° C . 53° D . 37°

答案解析收藏纠错 + 选题
5. (2020·杭州模拟) 在Rt△ABC中，∠C=90°，AC=1，AB=3，下列结论正确的是（）

A . sin B= $\text{[math]}$ B . BC=3sinB C . tan B= $\text{[math]}$ D . cosB= $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020·杭州模拟) 已知A、B两地之间铁路长为450千米，动车比火车每小时多行驶50千米，从A地到B地乘动车比乘火车少用40分钟，设动车速度为每小时x千米，则可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020·杭州模拟) 如图，点D是△ABC的边BC上一点，∠BAD=∠C，AC=2AD，如果△ACD的面积为15，那么△ABD的面积为（）

A . 5 B . 7.5 C . 10 D . 15

答案解析收藏纠错 + 选题
8. (2020·杭州模拟) 5G网络是第五代移动通信网络，它将推动我国数字经济发展迈上新台阶。据预测，2020年到2030年中国5G直接经济产出和间接经济产出的情况如图所示，根据图中提供的信息，下列推断不合理的是（）

A . 2030年5G间接经济产出比5G直接经济产出多4.2万亿元 B . 2020年到2030年，5G直接经济产出和5G间接经济产出都是逐年增长 C . 2030年5G直接经济产出约为2020年5G直接经济产出的13倍 D . 2022年到2023年与2023年到2024年5G间接经济产出的增长率相同

答案解析收藏纠错 + 选题
9. (2020·杭州模拟) 如果A(-2，n)，B(2，n)，C(4，n+24)这三个点都在同一个函数的图象上，那么这个函数的解析式可能是（）

A . y=2x B . y= $\text{[math]}$ C . y=-x² D . y=2x²

答案解析收藏纠错 + 选题
10. (2020·杭州模拟) 如图，在矩形ABCD中，AB=4，以AB为直径在矩形内作半圆，DF切该半圆于点E，点F在边BC上．设BF=x，y=tan∠CDF，则（）

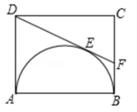
A . x²+4xy=4 B . x²-4xy=4 C . xy=4 D . xy+x²=4

答案解析收藏纠错 + 选题

二、填空题：本大题有6个小题，每小题4分，共24分。

11. (2020·杭州模拟) 若点(2，a)与点(b，-1)关于原点对称，则ab= 。

答案解析收藏纠错 + 选题
12. (2020·杭州模拟) 因式分解：2(x-y)²-4y(y-x)=。

答案解析收藏纠错 + 选题
13. (2020·杭州模拟) 一个密码箱的密码，每个数位上的数都是从0到9的自然数，若要使不知道密码的人一次就拨对密码的概率小于 $\text{[math]}$ ，则密码的位数至少需要位。

答案解析收藏纠错 + 选题
14. (2020·衢州模拟) 如图，圆锥的底面半径r为6cm，高h为8cm，则圆锥的侧面积为。

答案解析收藏纠错 + 选题
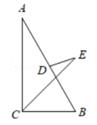
15. (2020·杭州模拟) 如图，在△ABC中，∠ACB=90°，∠B=60°，AB=4，D为AB的中点，CE平分∠ACB，∠DEC=30°，则DE=。

答案解析收藏纠错 + 选题
16. (2020·杭州模拟) 已知关于x的方程x+1= $\text{[math]}$ 的解满足方程x²+mx-1=k(1<m≤2)，则k的取值范围是。

答案解析收藏纠错 + 选题

三、解答题：本大题有7个小题，共66分．解答应写出文字说明、证明过程或演算步骤．

17. (2020·杭州模拟) 解方程： $\text{[math]}$
小红的解答过程如下：

解：去分母，得2(2x+1)-5x-1=1，①

去括号，得4x+2-5x-1=1，②

移项，得4x-5x=1-2+1，③

合并同类项，得-x=0，④

系数化为1，得x=0⑤

小红的解答正确吗？如果不正确，写出正确的解题过程。

答案解析收藏纠错 + 选题
18. (2020·杭州模拟) 如图，在△ABC中，点D，E分别在边AB，AC上，且AD=3，AC=6，AE=4，AB=8。
1. （1）求证：△ABC∽△AED。
2. （2）若BC=7，求线段DE的长。
答案解析收藏纠错 + 选题

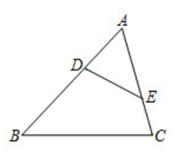
19. (2020·杭州模拟) 如图，为了了解我市中学生参加“科普知识”竞赛成绩的情况，随机抽查了部分参赛学生的成绩，整理并制作出如下的统计表和统计图。

组别	分数段(分)	频数
A组	60~70	30
B组	70~80	90
C组	80~90	m
D组	90~100	60

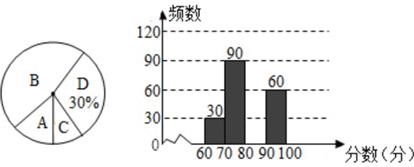
请根据图表信息，解答下列问题：

（1）求m的值。
（2）若A组学生的平均分是65分，B组学生的平均分是75分，C组学生的平均分是85分，D组学生的平均分是95分，请你估计参加本次竞赛的同学们的平均成绩是多少分？

答案解析收藏纠错 + 选题

20. (2020·杭州模拟) 已知等腰三角形的周长为12cm，底边长为xcm，腰长为ycm。
1. （1）求y关于x的函数表达式。
2. （2）当x，y均为整数时，求等腰三角形的面积。
答案解析收藏纠错 + 选题
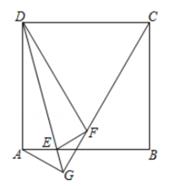
21. (2020·杭州模拟) 如图，在正方形ABCD中，点E为AB上的点(不与A，B重合)，△ADE与△FDE关于DE对称，作射线CF，与DE的延长线相交于点G，连结AG。
1. （1）当点E在AB上移动时，∠DGC的度数是否发生变化？若不变化，求出∠DGC的度数；若变化，请说明理由。
2. （2）当∠ADE=15°时，求 $\text{[math]}$ 的值。
答案解析收藏纠错 + 选题
22. (2020·杭州模拟) 已知一次函数y=-x+b(b是常数)。
1. （1）若b=1，求x为何值时y<0。
2. （2）若第四象限的点A(2b，b²-2)在该一次函数图象上，
  ①求b的值。
  
  ②设m=(x-2)(y-2)，当-2<x≤3时，求m的取值范围。
答案解析收藏纠错 + 选题
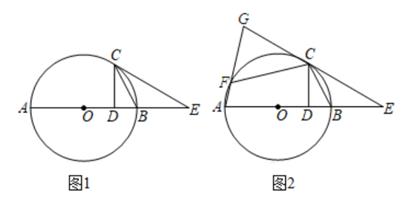
23. (2020·杭州模拟) 如图1，AB为⊙O的直径，C为⊙O上一点，连结CB，过C作CD⊥AB于点D，过点C作∠BCE，使∠BCE=∠BCD，其中CE交AB的延长线于点E。
1. （1）求证：CE是⊙O的切线。
2. （2）如图2，点F在⊙O上，且满足∠FCE=2∠ABC，连结AF并延长，交EC的延长线于点G。
  ①试探究线段CF与CD之间的数量关系。
  
  ②若CD=4，BD=2，求线段FG的长。
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

浙江省杭州市2020年数学中考复习卷（一）

副标题：

*注意事项：

浙江省杭州市2020年数学中考复习卷（一）

试题分析

总体分析

题量分析

难度分析

知识点分析