一、选择题(本题有10小题,每小题3分,共30分)
-
-
A . 3x-2x=x
B . 3x+2x=5x²
C . 3x·2x=6x
D . 3x÷2x= 
-
3.
(2022·长春模拟)
如图是由5个完全相同的小正方体搭成的几何体,如果将小正方体A放到小正方体B的正上方,则它的( )
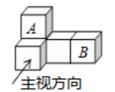
A . 左视图会发生改变,其他视图不变
B . 俯视图会发生改变,其他视图不变
C . 主视图会发生改变,其他视图不变
D . 三种视图都会发生改变
-
-
5.
(2020·衢州模拟)
小明要给朋友小林打电话,电话号码是七位正整数,他只记住了电话号码的前四位,后三位是由3,6,7三个数字组成的,但具体顺序不能确定,那么小明第一次就拨对的概率是( )
-
6.
(2022七下·济南期末)
在我国古代数学著作《九章算术》“勾股”章中有一题:“今有开门去阃(kǔn)一尺,不合二寸,问门广几何?”大意是说:如图,推开双门(AD和BC),门边缘D、C两点到门槛AB的距离为1尺(1尺=10寸),双门间的缝隙CD为2寸,那么门的宽度(两扇门的和)AB为( )
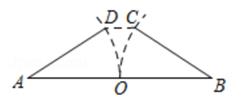
A . 103寸
B . 102寸
C . 101寸
D . 100寸
-
7.
(2020·衢州模拟)
如图,点A,B,D,C是⊙O上的四个点,连结AB,CD并延长,相交于点E,若∠BOD=20°, ∠AOC=90°,则∠E的度数为( )
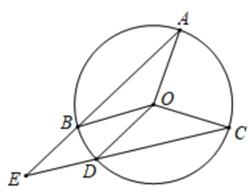
A . 30°
B . 35°
C . 45°
D . 55°
-
8.
(2020·衢州模拟)
如图,在平面直角坐标系中,矩形ABCD四个顶点的坐标分别为A(-1,2),B(-1,-1),C(3,-1),D(3,2),当双曲线y=

(k>0)与矩形有四个交点时,k的取值范围是( )
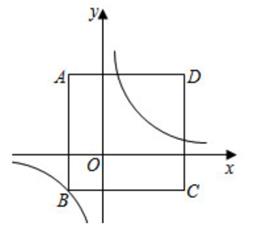
A . 0<k<2
B . 1<k<4
C . k>1
D . 0<k<1
-
9.
(2020九上·湖州月考)
如图,边长为2的正方形ABCD,点P从点A出发以每秒1个单位长度的速度沿A-D-C的路径向点C运动,同时点Q从点B出发以每秒2个单位长度的速度沿B-C-D-A的路径向点A运动,当点Q到达终点时,点P停止运动,设△PQC的面积为S,运动时间为t秒,则能大致反映S与t的函数关系的图象是( )
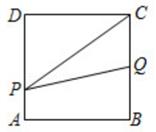
-
10.
(2020·衢州模拟)
如图,分别以Rt△ABC的直角边AC,斜边AB为边向外作等边△ACD和等边△ABE,F为AB的中点,连结DF,EF,∠ACB=90°,∠ABC=30°,则以下4个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④

其中正确的是( )
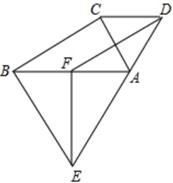
A . ①②
B . ①②③
C . ③④
D . ①②③④
二、填空题(本题共有6小题,每小题4分,共24分)
-
-
-
-
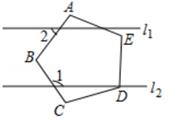
14.
(2020·衢州模拟)
如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC,CD于点P,Q,平行四边形ABCD的面积为6,则图中阴影部分的面积为
。
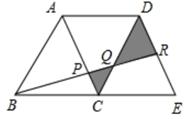
-
15.
(2020·衢州模拟)
如图,在Rt△ABC中,∠CAB=90°,AB=AC=2

,顶点A在y轴上,顶点C在反比例函数y=

(x>0)的图象上,已知点C的纵坐标是3,则经过点B的反比例函数的解析式为
。
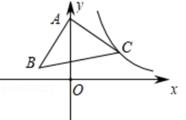
-
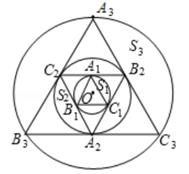
16.
(2020·衢州模拟)
如图,小圆O的半径为1,△A
1B
1C
1 , △A
2B
2C
2 , △A
3B
3C
3 , …,△A
nB
nC
n依次为同心圆O的内接正三角形和外切正三角形,由弦A
1C
1和弧A
1C
1围成的弓形面积记为S
1 , 由弦A
2C
2和弧A
2C
2围成的弓形面积记为S
2 , …,由弦A
nC
n和弧A
nC
n围成的弓形面积记为S
n , 其中由弦A
2020C
2020和弧A
2020C
2020围成的弓形面积S
2020为
。
三、解答题(本题共有8小题,第17~19小题每小题6分,第20~21小题每小题8分,第22~23小题每小题10分,第24小题12分,共66分。请务必写出解答过程)
-
-
-
-
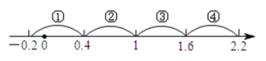
(2)
如图,若m为正整数,则该分式的值对应的点落在数轴上的第
段上。(填写序号即可)
-
19.
(2020·衢州模拟)
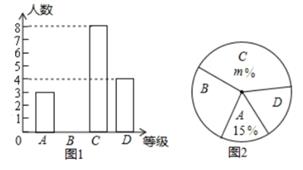
为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的不完整的统计图,请你根据统计图解答下列问题:
-
(1)
参加比赛的学生共有多少人?并补全图1的条形统计图.
-
(2)
在图2的扇形统计图中,m的值为,表示“D等级”的扇形的圆心角为度。
-
(3)
组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中有1名男生,2名女生,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率。
-
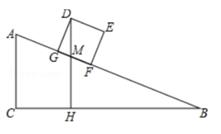
20.
(2020九上·襄汾期中)
有一个坡度i=1:2的斜坡AB,顶部A处的高AC为4米,B、C在同一水平地面上,其横截面如图。
-
-
(2)
现有一个侧面图为矩形DEFG的长方体货柜,其中DE=2.5米,EF=2米,该货柜沿斜坡向下时,点D离BC所在水平面的高度不断变化,求当BF=3.5米时,点D离BC所在水平面的高度DH。
-
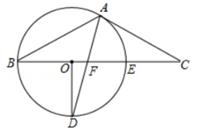
21.
(2020·衢州模拟)
如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连结AD交BC于点F,若AC=FC。
-
-
(2)
若BF=4,DF=

,求⊙O的半径。
-
-
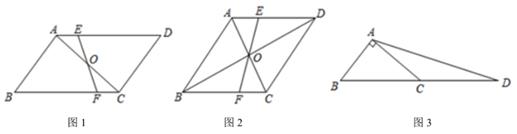
(1)
【猜想】如图1,在平行四边形ABCD中,点是对角线AC的中点,过点O的直线分别交AD,BC于点E,F。若平行四边形ABCD的面积是8,则四边形CDEF的面积是。
-
(2)
【探究】如图2,在菱形ABCD中,对角线相交于点O,过点O的直线分别交AD,BC于点E,F,若AC=5,BD=10,求四边形ABFE的面积。
-
(3)
【应用】如图3,在Rt△ABC中,∠BAC=90°,延长BC到点D,使DC=BC,连结AD,若AC=3,AD=2

,则△ABD的面积是
。
-
23.
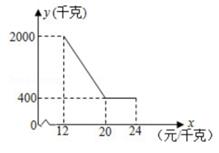
(2020·衢州模拟)
衢州某科技生态农业养殖有限公司种植和销售一种绿色羊肚菌,已知该羊肚菌的成本是12元/千克,规定销售价格不得低于成本,且不能高于成本的两倍。经过市场调查发现,某天该羊肚菌的销售量y(千克)与销售价格x(元/千克)之间的函数关系如下图所示。
-
-
-
(3)
若该公司按每销售一千克提取1元用于捐资助学,且保证每天的销售利润不低于3600元,则该羊肚菌销售价格该如何确定?
-
-
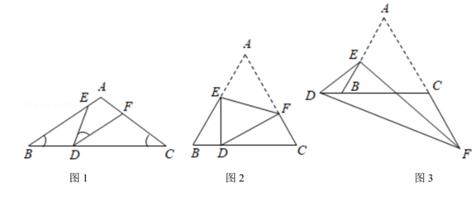
(1)
模型探究:如图1,D、E、F分别为△ABC三边BC、AB、AC上的点,且∠B=∠C=∠EDF=a。△BDE与△CFD相似吗?请说明理由。
-
(2)
模型应用:△ABC为等边三角形,其边长为8,E为AB边上一点,F为射线AC上一点,将△AEF沿EF翻折,使A点落在射线CB上的点D处,且BD=2。
①如图2,当点D在线段BC上时,求  的值。
的值。
②如图3,当点D落在线段CB的延长线上时,求△BDE与△CFD的周长之比。
 B .
B .  C .
C .  D .
D . 

 B .
B .  C .
C . 




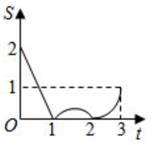 B .
B . 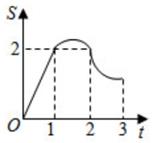 C .
C .  D .
D . 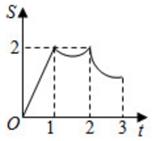









的值。