浙江省湖州市三校2021届九年级上学期数学第一次月考试卷

更新时间：2020-11-15 浏览次数：118 类型：月考试卷

一、选择题（共10题；共30分）

1. (2024九上·新会开学考) 下列事件中，为必然事件的是（）

A . 明天要下雨 B . $\text{[math]}$ C . $\text{[math]}$ D . 打开电视机，它正在播广告

答案解析收藏纠错 + 选题
2. (2020九上·湖州月考) 有一个转盘如图，让转盘自由转动两次，则指针两次都落在黄色区域的概率是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2020九上·湖州月考) 如果将抛物线 $\text{[math]}$ 平移，使它与抛物线 $\text{[math]}$ 重合，那么平移的方式可以是（）

A . 向左平移 $\text{[math]}$ 个单位，向上平移 $\text{[math]}$ 个单位 B . 向左平移 $\text{[math]}$ 个单位，向下平移 $\text{[math]}$ 个单位 C . 向右平移 $\text{[math]}$ 个单位，向上平移 $\text{[math]}$ 个单位 D . 向右平移 $\text{[math]}$ 个单位，向下平移 $\text{[math]}$ 个单位

答案解析收藏纠错 + 选题
4. (2020九上·湖州月考) 二次函数y=x²-2的图象是一条抛物线，下列关于该抛物线的说法正确的是（）

A . 抛物线开口向下 B . 当 $\text{[math]}$ 时，函数的最大值是-2 C . 抛物线的对称轴是直线 x=2 D . 抛物线与x轴有两个交点

答案解析收藏纠错 + 选题
5. (2020九上·湖州月考) 如图所示的是二次函数 $\text{[math]}$ 图象的一部分，其对称轴是 $\text{[math]}$ 且过点 $\text{[math]}$ 则下列选项中错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020九上·湖州月考) 在一只不透明的口袋中放入只有颜色不同的白球6个，黑球4个，黄球n个，搅匀后随机从中摸取1个恰好是白球的概率为 $\text{[math]}$ ，则放入的黄球总数为（）

A . 5个 B . 6个 C . 8个 D . 10个

答案解析收藏纠错 + 选题
7. (2022·临沭模拟) 小明在一次用频率估计概率的实验中，统计了某一结果出现的频率，并绘制了如图所示的统计图，则符合这一结果的实验可能是（）

A . 从一个装有2个白球和1个红球的不透明袋子中任意摸出一球（小球除颜色外，完全相同），摸到红球的概率 B . 掷一枚质地均匀的硬币，正面朝上的概率 C . 从一副去掉大小王的扑克牌，任意抽取一张，抽到黑桃的概率 D . 任意买一张电影票，座位号是2的倍数的概率

答案解析收藏纠错 + 选题
8. (2020九上·湖州月考) 如图，边长为2的正方形ABCD，点P从点A出发以每秒1个单位长度的速度沿A-D-C的路径向点C运动，同时点Q从点B出发以每秒2个单位长度的速度沿B-C-D-A的路径向点A运动，当点Ｑ到达终点时，点P停止运动，设△PQC的面积为S，运动时间为t秒，则能大致反映S与t的函数关系的图象是（）

A . B . C . D .

答案解析收藏纠错 + 选题
9. (2020九上·湖州月考) 在平面直角坐标系内，已知点A（﹣1，0），点B（1，1）都在直线y＝ $\text{[math]}$ x+ $\text{[math]}$ 上，若抛物线y＝ax²﹣x+1（a≠0）与线段AB有两个不同的交点，则a的取值范围是（　　）

A . a≤﹣2 B . a＜ $\text{[math]}$ C . 1≤a＜ $\text{[math]}$ 或a≤﹣2 D . ﹣2≤a＜ $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2020九上·湖州月考) 抛物线y＝ax²+bx+c的顶点为(﹣1，3)，与x轴的交点A在点(﹣3，0)和(﹣2，0)之间，其部分图象如图，则以下结论，其中符合题意结论的个数为（）
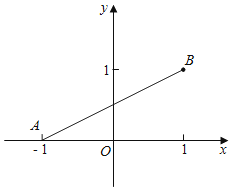
①若点P(﹣3，m)，Q(3，n)在抛物线上，则m＜n；②c＝a+3；③a+b+c＜0；④方程ax²+bx+c＝3有两个相等的实数根．

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题（共6题；共24分）

11. (2020九上·湖州月考) 小明从袋里（有红、黄、蓝、绿大小相同的四个球）随机一手抓两个球，则红、绿两球在一起的概率为。

答案解析收藏纠错 + 选题
12. (2020九上·湖州月考) 数学活动课上，老师拿来一个不透明的袋子，告诉学生里面装有4个除颜色外均相同的小球，并且球的颜色为红色和白色，让学生通过多次有放回的摸球，统计摸出红球和白球的次数，由此估计袋中红球和白球的个数．下面是全班分成的三个小组各摸球20次的结果，请你估计袋中有个红球．

摸到红球的次数

摸到白球的次数

一组

13

7

二组

14

6

三组

15

5

答案解析收藏纠错 + 选题
13. (2021九上·武汉期末) 抛物线y＝ax²﹣2ax﹣3与x轴交于两点，分别是（x₁ ， 0），（x₂ ， 0），则x₁+x₂＝.

答案解析收藏纠错 + 选题
14. (2020九上·湖州月考) 二次函数y＝ax²+bx+c（a≠0）的部分对应值如下表：

x

﹣3

﹣2

﹣1

0

1

2

y

﹣12

﹣5

0

3

4

3

利用二次函数的图象可知，当函数值y＞0时，x的取值范围是．

答案解析收藏纠错 + 选题
15. (2020九下·和平月考) 如图，假设篱笆（虚线部分）的长度是8m，则所围成矩形ABCD的最大面积是m.

答案解析收藏纠错 + 选题
16. (2020九上·仁寿期末) 已知二次函数y＝ax²+bx+c的图象如图所示，对称轴为直线x＝1，则下列结论：
①abc＞0；

②方程ax²+bx+c＝0的两根是x₁＝﹣1，x₂＝3；

③2a+b＝0；

④4a²+2b+c＜0，

其中正确结论的序号为．

答案解析收藏纠错 + 选题

三、解答题（共8题；共66分）

17. (2020九上·湖州月考) 2020 年 5 月 24 日习总书记参加湖北代表团审议时，提出了“织牢织密公共卫生防护网”的基本方针．现有一个不透明的口袋，其中装有四个小球，每个小球上标有一个汉字，分别是“织”“牢”“织”“密”，除汉字外其余均相同．搅匀后平安同学从口袋中随机摸出两个小球，请用画树状图（或列表）的方法，求平安同学摸出的两个小球中有“织”字且两个汉字不相同的概率．

答案解析收藏纠错 + 选题
18. (2022九上·江干月考) 一个不透明的布袋里装有4个只有颜色不同的球，其中3个红球，1个白球。
1. （1）从布袋中任意摸出1个球，求摸出是红球的概率；
2. （2）从布袋里摸出1个球，记下颜色后放回，搅匀，再摸出1个球，求两次摸出的球恰好颜色不同的概率（请用“画树状图”或“列表”等方法写出分析过程）。
答案解析收藏纠错 + 选题
19. (2022九上·西安期中) 一个智力挑战赛需要全部答对两道单项选择题，才能顺利通过第一关.第一道题有4个选项，第二道题有3个选项，这两道题小新都不会，不过小新还有一个“求助卡”没有用，使用“求助卡”可以让主持人去掉其中一题的一个错误选项.
1. （1）如果小新在第--题使用“求助卡”，请用树状图或者列表来分析小新顺利通过第一关的概率；
2. （2）从概率的角度分析，你建议小新在第几题使用“求助卡”.为什么.
答案解析收藏纠错 + 选题
20. (2020九上·北京期中) 在平面直角坐标系 $\text{[math]}$ 中，已知二次函数 $\text{[math]}$ 的图象与x轴交于点 $\text{[math]}$ ，与y轴交于点B ，将其图象在点A ， B之间的部分（含A ， B两点）记为F ．
1. （1）求点B的坐标及该函数的表达式；
2. （2）若二次函数 $\text{[math]}$ 的图象与F只有一个公共点，结合函数图象，求a的取值范围．
答案解析收藏纠错 + 选题
21. (2020九上·湖州月考) 高科技发展公司投资500万元，成功研制出一种市场需求量较大的高科技替代产品，并投入资金1500万元作为固定投资，已知生产每件产品的成本是40元.在销售过程中发现：当销售单价定为100元时，年销售量为20万件；销售单价每增加10元，年销售量将减少1万件，设销售单价为x（元），年销售量为y（万件），年获利（年获利=年销售额一生产成本—投资）为z（万元）.
1. （1）试写出y与x之间的函数关系式（不写x的取值范围）；
2. （2）试写出z与x之间的函数关系式（不写x的取值范围）；
3. （3）公司计划，在第一年按年获利最大确定销售单价进行销售；到第二年年底获利不低于1130万元，请借助函数的大致图象说明：第二年的销售单价x（元）应确定在什么范围内？
答案解析收藏纠错 + 选题

22. (2020九上·湖州月考) 为了解“停课不停学”期间，学生对线上学习方式的偏好情况，某校随机拍取40名学生进行问卷调查，其统计结果如表：

最喜欢的线上学习方式（没人最多选一种）	人数
直播	10
录播	$\text{[math]}$
资源包	5
线上答疑	8
合计	40

（1） $\text{[math]}$ ；
（2）若将选取各种“最喜欢的线上学习方式”的人数所占比例绘制成扇形统计图，求“直播"对应扇形的圆心角度数
（3）根据调查结果估计该校10000名学生中，最喜欢“线上答疑”的学生人数；
（4）在最喜欢“资源包”的学生中，有2名男生，3名女生.现从这5名学生中随机抽取2名学生介绍学习经验，求恰好抽到1名男生和1名女生的概率.

答案解析收藏纠错 + 选题

23. (2020九上·任城期中) 如图，已知二次函数 $\text{[math]}$ 与 $\text{[math]}$ 轴交于 $\text{[math]}$ 、 $\text{[math]}$ 两点（点 $\text{[math]}$ 位于点 $\text{[math]}$ 的左侧），与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，已知 $\text{[math]}$ 的面积是6．
1. （1）求 $\text{[math]}$ 的值；
2. （2）在抛物线上是否存在一点 $\text{[math]}$ ，使 $\text{[math]}$ ．存在请求出 $\text{[math]}$ 坐标，若不存在请说明理由．
答案解析收藏纠错 + 选题
24. (2020九上·湖州月考) 综合与探究
在平面直角坐标系中，抛物线y＝ $\text{[math]}$ x²+bx+c经过点A（﹣4，0），点M为抛物线的顶点，点B在y轴上，且OA＝OB ，直线AB与抛物线在第一象限交于点C（2，6），如图①．
1. （1）求抛物线的解析式；
2. （2）直线AB的函数解析式为，点M的坐标为，cos∠ABO＝；
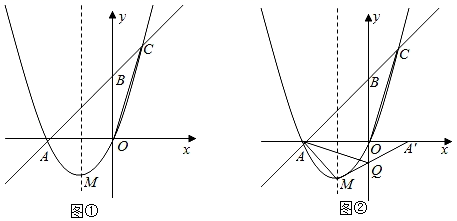
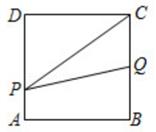
  连接OC ，若过点O的直线交线段AC于点P ，将△AOC的面积分成1：2的两部分，则点P的坐标为；
3. （3）在y轴上找一点Q ，使得△AMQ的周长最小．具体作法如图②，作点A关于y轴的对称点A'，连接MA'交y轴于点Q ，连接AM、AQ ，此时△AMQ的周长最小．请求出点Q的坐标；
4. （4）在坐标平面内是否存在点N ，使以点A、O、C、N为顶点的四边形是平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题