北京市海淀区2016-2017学年高考文数二模考试试卷

更新时间：2024-07-12 浏览次数：388 类型：高考模拟

一、选择题

1. (2017·海淀模拟) 若集合A={﹣2，0，1}，B={x|x＜﹣1或x＞0}，则A∩B=（）

A . {﹣2} B . {1} C . {﹣2，1} D . {﹣2，0，1}

答案解析收藏纠错 + 选题
2. (2017·海淀模拟) 在复平面内，复数 $\text{[math]}$ 对应的点的坐标为（）

A . （1，﹣1） B . （1，1） C . （﹣1，1） D . （﹣1，﹣1）

答案解析收藏纠错 + 选题
3. (2017·海淀模拟) 已知向量 $\text{[math]}$ =（x，1）， $\text{[math]}$ =（3，﹣2），若 $\text{[math]}$ ∥ $\text{[math]}$ ，则x=（）

A . ﹣3 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2017·海淀模拟) 执行如图所示的程序框图，若输入a=﹣7，d=3，则输出的S为（）

A . S=﹣12 B . S=﹣11 C . S=﹣10 D . S=﹣6

答案解析收藏纠错 + 选题
5. (2017·海淀模拟) 已知数列{a_n}是等比数列，则“a₂＞a₁”是“数列{a_n}为递增数列”的（）

A . 充分而不必要条件 B . 必要而不充分条件 C . 充分必要条件 D . 既不充分也不必要条件

答案解析收藏纠错 + 选题
6. (2017·海淀模拟) 北京市2016年12个月的PM2.5平均浓度指数如图所示．由图判断，四个季度中PM2.5的平均浓度指数方差最小的是（）

A . 第一季度 B . 第二季度 C . 第三季度 D . 第四季度

答案解析收藏纠错 + 选题
7. (2017·海淀模拟) 函数y=f（x）的图象如图所示，则f（x）的解析式可以为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2017·海淀模拟) 一位手机用户前四次输入四位数字手机密码均不正确，第五次输入密码正确，手机解锁．事后发现前四次输入的密码中，每次都有两个数字正确，但它们各自的位置均不正确．已知前四次输入密码分别为3406，1630，7364，6173，则正确的密码中一定含有数字（）

A . 4，6 B . 3，6 C . 3，7 D . 1，7

答案解析收藏纠错 + 选题

二、填空题

9. (2017·海淀模拟) 双曲线 $\text{[math]}$ 的实轴长为．

答案解析收藏纠错 + 选题
10. (2017·海淀模拟) 在log₂3，2^﹣3 ， cosπ这三个数中最大的数是．

答案解析收藏纠错 + 选题
11. (2017·海淀模拟) 在△ABC中，a=2，b=3，c=4，则其最大内角的余弦值为．

答案解析收藏纠错 + 选题
12. (2017·海淀模拟) 设D为不等式（x﹣1）²+y²≤1表示的平面区域，直线x+ $\text{[math]}$ y+b=0与区域D有公共点，则b的取值范围是．

答案解析收藏纠错 + 选题
13. (2017·海淀模拟) 已知O为原点，点P为直线2x+y﹣2=0上的任意一点．非零向量 $\text{[math]}$ =（m，n）．若 $\text{[math]}$ • $\text{[math]}$ 恒为定值，则 $\text{[math]}$ =．

答案解析收藏纠错 + 选题
14. (2017·海淀模拟) 如图，在棱长为1的正方体ABCD﹣A₁B₁C₁D₁中，点P是线段BD₁上的动点．当△PAC在平面DC₁ ， BC₁ ， AC上的正投影都为三角形时，将它们的面积分别记为S₁ ， S₂ ， S₃ ．
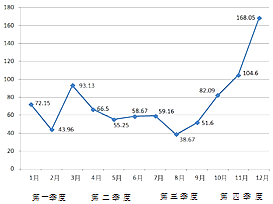
（i）当BP= $\text{[math]}$ 时，S₁S₂（填“＞”或“=”或“＜”）；
（ii） S₁+S₂+S₃的最大值为．

答案解析收藏纠错 + 选题

三、解答题

15. (2017·海淀模拟) 已知函数f（x）=sin2xcos $\text{[math]}$ ．
（Ⅰ）求函数f（x）的最小正周期和对称轴的方程；
（Ⅱ）求函数f（x）在区间 $\text{[math]}$ 上的最大值．

答案解析收藏纠错 + 选题
16. (2017·海淀模拟) 已知{a_n}是各项为正数的等差数列，S_n为其前n项和，且4S_n=（a_n+1）² ．
（Ⅰ）求a₁ ， a₂的值及{a_n}的通项公式；
（Ⅱ）求数列 $\text{[math]}$ 的最小值．

答案解析收藏纠错 + 选题
17. (2017·海淀模拟) 为了响应教育部颁布的《关于推进中小学生研学旅行的意见》，某校计划开设八门研学旅行课程，并对全校学生的选课意向进行调查（调查要求全员参与，每个学生必须从八门课程中选出唯一一门课程）．本次调查结果如下．图中，课程A，B，C，D，E为人文类课程，课程F，G，H为自然科学类课程．为进一步研究学生选课意向，结合上面图表，采取分层抽样方法从全校抽取1%的学生作为研究样本组（以下简称“组M”）．
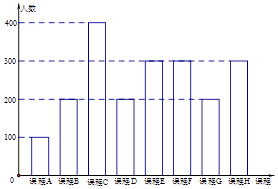
（Ⅰ）在“组M”中，选择人文类课程和自然科学类课程的人数各有多少？
（Ⅱ）某地举办自然科学营活动，学校要求：参加活动的学生只能是“组M”中选择F课程或G课程的同学，并且这些同学以自愿报名缴费的方式参加活动．选择F课程的学生中有x人参加科学营活动，每人需缴纳2000元，选择G课程的学生中有y人参加该活动，每人需缴纳1000元．记选择F课程和G课程的学生自愿报名人数的情况为（x，y），参加活动的学生缴纳费用总和为S元．
（ⅰ）当S=4000时，写出（x，y）的所有可能取值；
（ⅱ）若选择G课程的同学都参加科学营活动，求S＞4500元的概率．

答案解析收藏纠错 + 选题
18. (2017·海淀模拟) 如图，在四棱锥P﹣ABCD中，底面ABCD为菱形，PC⊥平面ABCD，点E在棱PA上．
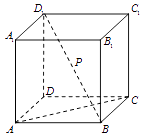
（Ⅰ）求证：直线BD⊥平面PAC；
（Ⅱ）若PC∥平面BDE，求证：AE=EP；
（Ⅲ）是否存在点E，使得四面体A﹣BDE的体积等于四面体P﹣BDC的体积的 $\text{[math]}$ ？若存在，求出 $\text{[math]}$ 的值；若不存在，请说明理由．

答案解析收藏纠错 + 选题
19. (2017·海淀模拟) 已知函数f（x）= $\text{[math]}$ ﹣2x+1．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）当0＜a≤ $\text{[math]}$ 时，求函数f（x）在区间[﹣a，a]上的最大值．

答案解析收藏纠错 + 选题
20. (2017·海淀模拟) 已知F₁（﹣1，0），F₂（1，0）分别是椭圆C： $\text{[math]}$ =1（a＞0）的左、右焦点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若A，B分别在直线x=﹣2和x=2上，且AF₁⊥BF₁ ．
（ⅰ）当△ABF₁为等腰三角形时，求△ABF₁的面积；
（ⅱ）求点F₁ ， F₂到直线AB距离之和的最小值．

答案解析收藏纠错 + 选题