一、单选题（本题共12小题，每小题3分，满分36分，中每小题给出的四个选项中，只有一项符合题目要求的，请将正确选则项请的字母代号填涂在答题卷相应位置上）
-
1.
﹣5的绝对值是（ ）
A . ﹣5
B . 
C . 
D . 5
-
2.
恩施气候独特，土壤天然含硒，盛产茶叶，恩施富硒茶叶2013年总产量达64000吨，将64000用科学记数法表示为（ ）
-
3.
如图，已知AB∥DE，∠ABC=70°，∠CDE=140°，则∠BCD的值为（ ）
A . 20°
B . 30°
C . 40°
D . 70°
-
4.
函数y=
+x﹣2的自变量x的取值范围是（ ）
A . x≥2
B . x＞2
C . x≠2
D . x≤2
-
-
6.
某中学开展“阳光体育一小时”活动，根据学校实际情况，如图决定开设“A：踢毽子，B：篮球，C：跳绳，D：乒乓球”四项运动项目（每位同学必须选择一项），为了解学生最喜欢哪一项运动项目，随机抽取了一部分学生进行调查，丙将调查结果绘制成如图的统计图，则参加调查的学生中最喜欢跳绳运动项目的学生数为（ ）
A . 240
B . 120
C . 80
D . 40
-
7.
如图是一个正方体纸盒的展开图，其中的六个正方形内分别标有数字“0”、“1”、“2”、“5”和汉字、“数”、“学”，将其围成一个正方体后，则与“5”相对的是（ ）
A . 0
B . 2
C . 数
D . 学
-
8.
关于x的不等式组
的解集为x＜3，那么m的取值范围为（ ）
A . m=3
B . m＞3
C . m＜3
D . m≥3
-
9.
(2020九上·双清期末)
如图，在平行四边形ABCD中，EF∥AB交AD于E，交BD于F，DE：EA=3：4，EF=3，则CD的长为（ ）
A . 4
B . 7
C . 3
D . 12
-
10.
如图，AB是⊙O的直径，弦CD交AB于点E，且E为OB的中点，∠CDB=30°，CD=4
， 则阴影部分的面积为（ ）
-
11.
(2021七上·上思期中)
随着服装市场竞争日益激烈，某品牌服装专卖店一款服装按原售价降价
a元后，再次降价20%，现售价为
b元，则原售价为（ ）
A . 
元
B . （ 
）元
C . （ 
）元
D . （ 
）元
-
12.
如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为直线x=﹣1，给出四个结论：
①b2＞4ac；②2a+b=0；③a+b+c＞0；④若点B（﹣
， y1）、C（﹣
， y2）为函数图象上的两点，则y1＜y2 ，
其中正确结论是（ ）
A . ②④
B . ①④
C . ①③
D . ②③
二、填空题（共4小题，每小题3分，满分12分，不要求写出解答过程，请把答案直接填写在答题卷相应位置上）
-
-
-
15.
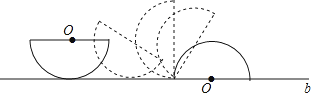
如图，半径为5的半圆的初始状态是直径平行于桌面上的直线b，然后把半圆沿直线b进行无滑动滚动，使半圆的直径与直线b重合为止，则圆心O运动路径的长度等于 ．
-
16.
观察下列一组数：1，2，2，3，3，3，4，4，4，4，5，5，5，5，5，6，…其中每个数n都连续出现n次，那么这一组数的第119个数是 ．
三、解答题（本大题共8小题，满分72分，请在大题卷指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
-
17.
先化简，再求值：
， 其中x=2
﹣1．
-
18.
如图，四边形ABCD、为正方形，连接AG、CE.
-
-
-
19.
质地均匀的小正方体，六个面分别有数字“1”、“2”、“3”、“4”、“5”、“6”，同时投掷两枚，观察朝上一面的数字．
-
-
-
20.
(2020·武威模拟)
如图，某渔船在海面上朝正西方向以20海里/时匀速航行，在A处观测到灯塔C在北偏西60°方向上，航行1小时到达B处，此时观察到灯塔C在北偏西30°方向上，若该船继续向西航行至离灯塔距离最近的位置，求此时渔船到灯塔的距离。（结果精确到1海里，参考数据：≈1.732）
-
21.
如图，已知点A、P在反比例函数y=
（k＜0）的图象上，点B、Q在直线y=x﹣3的图象上，点B的纵坐标为﹣1，AB⊥x轴，且S△OAB=4，若P、Q两点关于y轴对称，设点P的坐标为（m，n）．
-
-
（2）
求
的值．
-
22.
某工厂现有甲种原料360千克，乙种原料290千克，计划用这两种原料全部生产A、B两种产品共50件，生产A、B两种产品与所需原料情况如下表所示：
原料型号
| 甲种原料（千克）
| 乙种原料（千克）
|
A产品（每件）
| 9
| 3
|
B产品（每件）
| 4
| 10
|
-
-
（2）
若生成一件A产品可获利80元，生产一件B产品可获利120元，怎样安排生产可获得最大利润？
-
23.
如图，AB是⊙O的直径，AB=6，过点O作OH⊥AB交圆于点H，点C是弧AH上异于A、B的动点，过点C作CD⊥OA，CE⊥OH，垂足分别为D、E，过点C的直线交OA的延长线于点G，且∠GCD=∠CED．
-
-
-
（3）
过点C作CF⊥DE于点F，若∠CED=30°，求CF的长．
-
24.
矩形AOCD绕顶点A（0，5）逆时针方向旋转，当旋转到如图所示的位置时，边BE交边CD于M，且ME=2，CM=4．
-
-
-
-
（4）
在抛物线上是否存在点P，使S
△PAM=
？若存在，求出P点坐标；若不存在，请说明理由．
