广西钦州市钦北区2016-2017高一下学期物理期末考试试卷

如图所示，由于地球的自转，地球表面上P、Q两物体均绕地球自转轴做匀速圆周运动．

对于P、Q两物体的运动，下列说法正确的是（   ）

公路上的拱形桥是常见的，汽车过桥最高点时的运动可以看做匀速圆周运动．如图所示，汽车通过桥最高点时（   ）

如图所示，用细线吊着一个质量为m的小球，使小球在水平面内做圆锥摆运动，关于小球受力，正确的是（   ）

如图所示，实线圆表示地球，竖直虚线a表示地轴，虚线圆b、c、d、e表示地球卫星可能的轨道，对于此图，下列说法正确的是（   ）

质点所受的力F随时间变化的规律如图所示，力的方向始终在一直线上．已知t=0时质点的速度为零．在图中所示的t₁、t₂、t₃和t₄各时刻中，哪一时刻质点的动能最大（   ）

如图，以10m/s的水平速度抛出的物体，飞行一段时间后垂直撞在倾角为θ=30°的斜面上，空气阻力不计，则物体飞行的时间为（   ）

如图所示，一颗人造卫星原来在椭圆轨道1绕地球E运行，在P点变轨后进入轨道2做匀速圆周运动．下列说法正确的是（   ）

如图所示，重为G的物体静止在倾角为α的粗糙斜面体上，现使斜面体向右做匀速直线运动，通过的位移为x，物体相对斜面体一直保持静止，则在这个过程中（   ）

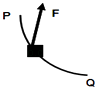
竖直平面内有两个半径不同的半圆形光滑轨道，如图所示，A、M、B三点位于同一水平面上，C、D分别为两轨道的最低点，将两个相同的小球分别从A、B处静止释放，当它们各自通过C、D时，则（   ）

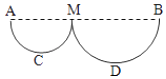
带有 光滑圆弧轨道、质量为M的滑车静止置于光滑水平面上，如图所示，一质量为m的小球以速度v₀水平冲上滑车，到达某一高度后，小球又返回车的左端．若M=2m，则（   ）

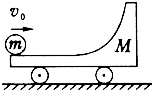
如图所示，用“碰撞实验器”可以验证动量守恒定律，即验证两个小球在水平轨道末端碰撞前后的动量守恒．入射小球质量为m₁ ， 被碰小球质量为m₂ ， O点是小球抛出点在水平地面上的投影．实验时，先让入射小球m₁多次从倾斜轨道上S位置静止释放，找到其平均落地点的位置，并记下此位置距O点的距离；然后把被碰小球m₂静置于水平轨道末端，再将入射小球m₁从倾斜轨道上S位置静止释放，与小球m₂相撞，多次重复此过程，并分别找到它们平均落点的位置距O点的距离．则下列说法正确的是（   ）

一个可视为质点的小球被长为L的绳悬挂于O点，空气阻力忽略不计，开始时绳与竖直方向的夹角为α，在球从A点由静止开始运动到等高点C点的过程中（B点是运动过程中的最低点），下列说法正确的是（   ）

如图所示，一个物体在与水平面的夹角为θ的斜向上的拉力F的作用下，沿光滑水平面做匀加速直线运动，在物体通过距离S的过程中运动的时间为t，则（   ）

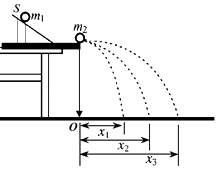
用如图1所示的装置，来验证碰撞过程中的动量守恒．图中PQ是斜槽，QR为水平槽．O点是水平槽末端R在记录纸上的垂直投影点，A、B两球的质量之比m_A：m_B=3：1．先使A球从斜槽上某一高度处由静止释放，在水平地面的记录纸上留下落点痕迹P，重复10次，得到10个落点．再把B球放在水平槽上的末端R处，让A球仍从同一高度处由静止释放，与B球碰撞，碰后A、B球分别在记录纸上留下各自的落点痕迹，重复10次．A、B两球在记录纸上留下的落点痕迹如图2所示，其中米尺的零点与O点对齐．

利用图1装置做“验证机械能守恒定律”实验．

某同学用如图甲所示的装置通过研究重锤的落体运动来验证机械能守恒定律．已知重力加速度为g．

如图所示，位于竖直平面内光滑的 圆弧轨道半径为R，轨道的最低点B的切线沿水平方向．质量为m的小球（可视为质点）从轨道最上端A点由静止释放．若空气阻力忽略不计，重力加速度为g．求：

如图所示，abc是光滑的轨道，其中ab是水平的，bc为与ab相切的位于竖直平面内的半圆，半径R=0.30m．质量m=0.20kg的小球A静止在轨道上，另一质量M=0.60kg、速度V₀=5.5m/s的小球B与小球A正碰．已知相碰后小球A经过半圆的最高点c落到轨道上距b点为，l=4 R处，重力加速度g=10m/s² ， 求：