2015年辽宁省辽阳市中考数学真题试卷

更新时间：2016-07-01 浏览次数：408 类型：中考真卷

一、选择题（本大题共8小题，每小题3分，共24分）

1. $\text{[math]}$ 的相反数是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. 下列计算正确的是（　　）

A . x²•x³=x⁶ B . x⁵+x⁵=2x¹⁰ C . （﹣2x）³=8x³ D . （﹣2x³）÷（﹣6x²）= $\text{[math]}$

答案解析收藏纠错 + 选题
3. 下列各图不是正方体表面展开图的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
4. 一组数据：2，3，6，6，7，8，8，8的中位数是（　　）

A . 6 B . 6.5 C . 7 D . 8

答案解析收藏纠错 + 选题
5.
如图，AD∥CB，∠D=43°，∠B=25°，则∠DEB的度数为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. 从甲地到乙地有两条公路，一条是全长450公里的普通公路，一条是全长330公里的高速公路，某客车在高速公路上行驶的平均速度比在普通公路上快35公里/小时，由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半．如果设该客车由高速公路从甲地到乙地所需时间为x小时，那么x满足的分式方程是（　　）

A . $\text{[math]}$ = $\text{[math]}$ $\text{[math]}$ B . $\text{[math]}$ = $\text{[math]}$ -35 C . $\text{[math]}$ - $\text{[math]}$ =35 D . $\text{[math]}$ ﹣ $\text{[math]}$ =35

答案解析收藏纠错 + 选题
7. (2020·郑州模拟)
如图，直线y=﹣x+2与y=ax+b（a≠0且a，b为常数）的交点坐标为（3，﹣1），则关于x的不等式﹣x+2≥ax+b的解集为（　　）

A . x≥﹣1 B . x≥3 C . x≤﹣1 D . x≤3

答案解析收藏纠错 + 选题
8. 下列事件为必然事件的是（　　）

A . 如果a，b是实数，那么a•b=b•a B . 抛掷一枚均匀的硬币，落地后正面朝上 C . 汽车行驶到交通岗遇到绿色的信号灯 D . 口袋中装有3个红球，从中随机摸出一球，这个球的白球

答案解析收藏纠错 + 选题
9. (2021九下·重庆开学考)
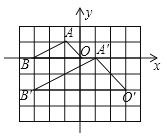
如图，在边长为1的小正方形组成的网格中，建立平面直角坐标系，△ABO与△A′B′O′是以点P为位似中心的位似图形，它们的顶点均在格点（网格线的交点）上，则点P的坐标为（　　）

A . （0，0） B . （0，1） C . （﹣3，2） D . （3，﹣2）

答案解析收藏纠错 + 选题
10.
如图，点A是双曲线 $\text{[math]}$ 在第二象限分支上的一个动点，连接AO并延长交另一分支于点B，以AB为底作等腰△ABC，且∠ACB=120°，点C在第一象限，随着点A的运动，点C的位置也不断变化，但点C始终在双曲线 $\text{[math]}$ 上运动，则k的值为（　　）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题

二、填空题（本大题共8小题，每小题3分，共24分）

11. 某工业园区，今年第一季度新开工94个项目，总投资7429亿元．请将7429亿，用科学记数法表示为．

答案解析收藏纠错 + 选题
12. (2024八上·成都开学考) $\text{[math]}$ 的整数部分是．

答案解析收藏纠错 + 选题
13.
如图，点A，B，C是⊙O上的点，AO=AB，则∠ACB= 度．

答案解析收藏纠错 + 选题
14. 某校组织“书香校园”读书活动，某班图书角现有文学书18本，科普书9本，人物传记12本，军事书6本，小明随机抽取一本，恰好是人物传记的概率是．

答案解析收藏纠错 + 选题
15. (2019九上·湖南开学考)
如图，在△ABC中，BD⊥AC于D，点E为AB的中点，AD=6，DE=5，则线段BD的长等于．

答案解析收藏纠错 + 选题
16. (2024八上·红桥期末) 一个多边形的内角和是外角和的2倍，则这个多边形的边数为．

答案解析收藏纠错 + 选题
17. (2019九下·江苏月考)
如图，在平面直角坐标系中，矩形OABC，OA=3，OC=6，将△ABC沿对角线AC翻折，使点B落在点B′处，AB′与y轴交于点D，则点D的坐标为．

答案解析收藏纠错 + 选题
18.
如图，△ABC，∠C=90°，AC=BC=a，在△ABC中截出一个正方形A₁B₁C₁D₁ ，使点A₁ ， D₁分别在AC，BC边上，边B₁C₁在AB边上；在△BC₁D₁在截出第二个正方形A₂B₂C₂D₂ ，使点A₂ ， D₂分别在BC₁ ， D₁C₁边上，边B₂C₂在BD₁边上；…，依此方法作下去，则第n个正方形的边长为．

答案解析收藏纠错 + 选题

三、解答题（第19题10分，第20题12分，共22分）

19. 先化简，再求值：[ $\text{[math]}$ ﹣ $\text{[math]}$ ]÷ $\text{[math]}$ ，请选取一个适当的x的数值代入求值．

答案解析收藏纠错 + 选题
20.
校文艺部在全校范围内随机抽取一部分同学，对同学们喜爱的四种“明星真人秀”节目进行问卷调查（每位同学只能选择一种最喜爱的节目），并将调查结果整理后分别绘制成如图所示的不完整的扇形统计图和条形统计图）．
请根据所给信息回答下列问题：
1. （1）本次问卷调查共调查了多少名学生？
2. （2）请将两幅统计图补充完整；
3. （3）若该校有1500名学生，据此估计有多少名学生最喜爱《奔跑吧兄弟》节目．
答案解析收藏纠错 + 选题

四、解答题（每小题12分，共24分）

21. 某宾馆准备购进一批换气扇，从电器商场了解到：一台A型换气扇和三台B型换气扇共需275元；三台A型换气扇和二台B型换气扇共需300元．
1. （1）求一台A型换气扇和一台B型换气扇的售价各是多少元；
2. （2）若该宾馆准备同时购进这两种型号的换气扇共40台并且A型换气扇的数量不多于B型换气扇数量的3倍，请设计出最省钱的购买方案，并说明理由．
答案解析收藏纠错 + 选题
22.
如图，码头A在码头B的正东方向，两个码头之间的距离为32海里，今有一货船由码头A出发，沿北偏西60°方向航行到达小岛C处，此时测得码头B在南偏东45°方向，求码头A与小岛C的距离．（ $\text{[math]}$ ≈1.732，结果精确到0.01海里）

答案解析收藏纠错 + 选题

五、解答题

23.
如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交BC，AC于点D，E，DG⊥AC于点G，交AB的延长线于点F．
1. （1）求证：直线FG是⊙O的切线；
2. （2）若AC=10，cosA= $\text{[math]}$ ，求CG的长．
答案解析收藏纠错 + 选题
24. 某商场试销一种商品，成本为每件200元，规定试销期间销售单价不低于成本单价，且获利不得高于50%，一段时间后，发现销售量y（件）与销售单价x（元）之间的函数关系如下表：
销售单价x（元）
…
230
235
240
245
…
销售量y（件）
…
440
430
420
410
…
1. （1）请根据表格中所给数据，求出y关于x的函数关系式；
2. （2）设商场所获利润为w元，将商品销售单价定为多少时，才能使所获利润最大？最大利润是多少？
答案解析收藏纠错 + 选题
25.
菱形ABCD中，两条对角线AC，BD相交于点O，∠MON+∠BCD=180°，∠MON绕点O旋转，射线OM交边BC于点E，射线ON交边DC于点F，连接EF．
1. （1）如图1，当∠ABC=90°时，△OEF的形状是　；
2. （2）如图2，当∠ABC=60°时，请判断△OEF的形状，并说明理由；
3. （3）
  在（1）的条件下，将∠MON的顶点移到AO的中点O′处，∠MO′N绕点O′旋转，仍满足∠MO′N+∠BCD=180°，射线O′M交直线BC于点E，射线O′N交直线CD于点F，当BC=4，且= $\text{[math]}$ 时，直接写出线段CE的长．
答案解析收藏纠错 + 选题
26.
如图1，平面直角坐标系中，直线y=﹣ $\text{[math]}$ x+3与抛物线y=ax²+ $\text{[math]}$ x+c相交于A，B两点，其中点A在x轴上，点B在y轴上．
1. （1）求抛物线的解析式；
2. （2）在抛物线上存在一点M，使△MAB是以AB为直角边的直角三角形，求点M的坐标；
3. （3）如图2，点E为线段AB上一点，BE=2，以BE为腰作等腰Rt△BDE，使它与△AOB在直线AB的同侧，∠BED=90°，△BDE沿着BA方向以每秒一个单位的速度运动，当点B与A重合时停止运动，设运动时间为t秒，△BDE与△AOB重叠部分的面积为S，直接写出S关于t的函数关系式，并写出自变量t的取值范围．
答案解析收藏纠错 + 选题