河南省百校2020年九年级数学中考大联考试卷

更新时间：2020-07-19 浏览次数：253 类型：中考模拟

一、单选题

1. (2020·河南模拟) $\text{[math]}$ 的相反数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020·河南模拟) 2020年2月14日，电影《刺猬索尼克》在美国上映，据悉，该片在首映当日就轻松将2100万美元票房收入囊中.数据“2100万”用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2020·河南模拟) 如图，小明用由5个相同的小立方体搭成的立体图形研究几何体的三视图的变化情况.若由图1变到图2，不变化的是（）

A . 主视图 B . 主视图和左视图 C . 主视图和俯视图 D . 左视图和俯视图

答案解析收藏纠错 + 选题
4. (2020·河南模拟) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021·宜宾模拟) 疫情无情人有情，爱心捐款传真情.新型冠状病毒感染的肺炎疫情期间，某班学生积极参加献爱心活动，该班50名学生的捐款统计情况如下表：

金额/元

5

10

20

50

100

人数

6

17

14

8

5

则他们捐款金额的平均数和中位数分别是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021九上·自贡期末) 关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的根的情况是（）

A . 有两个相等的实数根 B . 有两个不相等的实数根 C . 没有实数根 D . 无法确定

答案解析收藏纠错 + 选题
7. (2020·河南模拟) 如果点 $\text{[math]}$ 是抛物线 $\text{[math]}$ 上两个不同的点，那么 $\text{[math]}$ 的值为（）

A . 4 B . 5 C . 6 D . 7

答案解析收藏纠错 + 选题
8. (2021九上·开福期末) 疫情防控，我们一直在坚守.某居委会组织两个检查组，分别对“居民体温”和“居民安全出行”的情况进行抽查.若这两个检查组在辖区内的某三个校区中各自随机抽取一个小区进行检查，则他们恰好抽到同一个小区的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020·河南模拟) 如图，已知 $\text{[math]}$ ，以点 $\text{[math]}$ 为圆心，适当长度为半径作弧，分别交边 $\text{[math]}$ 于点 $\text{[math]}$ ，分别以 $\text{[math]}$ 为圆心，大于 $\text{[math]}$ 的长为半径作弧，两弧在 $\text{[math]}$ 内交于点 $\text{[math]}$ ，作射线 $\text{[math]}$ .若 $\text{[math]}$ 是 $\text{[math]}$ 上一点，过点 $\text{[math]}$ 作 $\text{[math]}$ 的平行线交 $\text{[math]}$ 于点 $\text{[math]}$ ，且 $\text{[math]}$ ，则直线 $\text{[math]}$ 与 $\text{[math]}$ 之间的距离是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 3 D . 6

答案解析收藏纠错 + 选题
10. (2020·河南模拟) 如图，已致点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 轴的正半轴上，且 $\text{[math]}$ .过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ；过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ；过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ；……；按此规律进行下去，则点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2020·河南模拟) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2022九下·安顺月考) 如图， $\text{[math]}$ ，垂足为 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为.

答案解析收藏纠错 + 选题
13. (2020·河南模拟) 不等式组 $\text{[math]}$ ，的所有整数解的和是.

答案解析收藏纠错 + 选题
14. (2020·河南模拟) 如图，扇形 $\text{[math]}$ 的圆心角为 $\text{[math]}$ ，半径为8，将扇形 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转得到扇形 $\text{[math]}$ ，点 $\text{[math]}$ 的对应点分别为 $\text{[math]}$ .若点 $\text{[math]}$ 刚好落在 $\text{[math]}$ 上，则阴影部分的面积为.

答案解析收藏纠错 + 选题
15. (2020·河南模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 边上的中点， $\text{[math]}$ 是 $\text{[math]}$ 边上任意一点，且 $\text{[math]}$ .若点 $\text{[math]}$ 关于直线 $\text{[math]}$ 的对称点 $\text{[math]}$ 恰好落在 $\text{[math]}$ 的中位线上，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题

三、解答题

16. (2020·河南模拟) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ .

答案解析收藏纠错 + 选题
17. (2021·灞桥模拟) 某学校为了丰富学生课余生活，开展了“第二课堂”活动，推出了以下四种选修课程： $\text{[math]}$ .绘画； $\text{[math]}$ .唱歌； $\text{[math]}$ .跳舞； $\text{[math]}$ .演讲； $\text{[math]}$ .书法.学校规定：每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生，对他们选择的课程情况进行了统计，并绘制了如下两幅不完整的统计图.

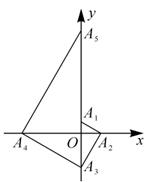
请结合统计图中的信息解决下列问题：
1. （1）这次抽查的学生人数是多少人？
2. （2）将条形统计图补充完整.
3. （3）求扇形统计图中课程 $\text{[math]}$ 所对应扇形的圆心角的度数.
4. （4）如果该校共有1200名学生，请你估计该校选择课程 $\text{[math]}$ 的学生约有多少人.
答案解析收藏纠错 + 选题
18. (2020·河南模拟) 如图， $\text{[math]}$ 是☉ $\text{[math]}$ 的直径， $\text{[math]}$ 为☉ $\text{[math]}$ 上一点， $\text{[math]}$ 是半径 $\text{[math]}$ 上一动点（不与 $\text{[math]}$ 重合），过点 $\text{[math]}$ 作射线 $\text{[math]}$ ，分别交弦 $\text{[math]}$ ， $\text{[math]}$ 于 $\text{[math]}$ 两点，过点 $\text{[math]}$ 的切线交射线 $\text{[math]}$ 于点 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ .
2. （2）当 $\text{[math]}$ 是 $\text{[math]}$ 的中点时，
  ①若 $\text{[math]}$ ，判断以 $\text{[math]}$ 为顶点的四边形是什么特殊四边形，并说明理由；
  
  ②若 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ _▲_.
答案解析收藏纠错 + 选题
19. (2020·河南模拟) 如图，一次函数 $\text{[math]}$ 的图像与反比例函数 $\text{[math]}$ 的图像交于 $\text{[math]}$ ， $\text{[math]}$ 两点，与 $\text{[math]}$ 轴分别交于 $\text{[math]}$ 两点，且 $\text{[math]}$ .
1. （1）求一次函数和反比例函数的解析式；
2. （2）若点 $\text{[math]}$ 与点 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称，连接 $\text{[math]}$ ，求 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
20. (2020·沭阳模拟) 如图， $\text{[math]}$ 是垂直于水平面的一座大楼，离大楼30米（ $\text{[math]}$ 米）远的地方有一段斜坡 $\text{[math]}$ （坡度为 $\text{[math]}$ ），且坡长 $\text{[math]}$ 米.某时刻，在太阳光的照射下，大楼的影子落在了水平面 $\text{[math]}$ 、斜坡 $\text{[math]}$ 、以及坡顶上的水平面 $\text{[math]}$ 处（ $\text{[math]}$ 均在同一个平面内）.若 $\text{[math]}$ 米，且此时太阳光与水平面所夹锐角为 $\text{[math]}$ （ $\text{[math]}$ ），试求出大楼 $\text{[math]}$ 的高.（参考数据： $\text{[math]}$ ）

答案解析收藏纠错 + 选题
21. (2020·河南模拟) 某超市销售一种商品，成本价为50元/千克，规定每千克售价不低于成本价，且不高于85元.经过市场调查，该商品每天的销售量 $\text{[math]}$ （千克）与售价 $\text{[math]}$ （元/千克）满足一次函数关系，部分数据如下表：

售价 $\text{[math]}$ （元/千克）

50

60

70

销售量 $\text{[math]}$ （千克）

120

100

80
1. （1）求 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数表达式.
2. （2）设该商品每天的总利润为 $\text{[math]}$ （元），则当售价 $\text{[math]}$ 定为多少元/千克时，超市每天能获得最大利润？最大利润是多少元？
3. （3）如果超市要获得每天不低于1600元的利润，且符合超市自己的规定，那么该商品的售价 $\text{[math]}$ 的取值范围是多少？请说明理由.
答案解析收藏纠错 + 选题
22. (2020·河南模拟) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是平面内不与点 $\text{[math]}$ 重合的任意一点，连接 $\text{[math]}$ ，将线段 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 得到线段 $\text{[math]}$ ，连接 $\text{[math]}$ 是 $\text{[math]}$ 的中点， $\text{[math]}$ 是 $\text{[math]}$ 的中点.
1. （1）问题发现：
  如图1，当 $\text{[math]}$ 时， $\text{[math]}$ 的值是，直线 $\text{[math]}$ 与直线 $\text{[math]}$ 相交所成的较小角的度数是.
2. （2）类比探究：
  如图2，当 $\text{[math]}$ 时，请写出 $\text{[math]}$ 的值及直线 $\text{[math]}$ 与直线 $\text{[math]}$ 相交所成的较小角的度数，并说明理由.
3. （3）解决问题：
  如图3，当 $\text{[math]}$ 时，若 $\text{[math]}$ 是 $\text{[math]}$ 的中点，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，且点 $\text{[math]}$ 在同一条直线上，请直接写出 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
23. (2020·河南模拟) 如图，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴相交于 $\text{[math]}$ 两点（点 $\text{[math]}$ 位于点 $\text{[math]}$ 的左侧），与 $\text{[math]}$ 轴相交于点 $\text{[math]}$ ， $\text{[math]}$ 是抛物线的顶点，直线 $\text{[math]}$ 是抛物线的对称轴，且点 $\text{[math]}$ 的坐标为 $\text{[math]}$ .
1. （1）求抛物线的解析式.
2. （2）已知 $\text{[math]}$ 为线段 $\text{[math]}$ 上一个动点，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴于点 $\text{[math]}$ .若 $\text{[math]}$ 的面积为 $\text{[math]}$ .
  ①求 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系式，并写出自变量 $\text{[math]}$ 的取值范围；
  
  ②当 $\text{[math]}$ 取得最值时，求点 $\text{[math]}$ 的坐标.
3. （3）在（2）的条件下，在线段 $\text{[math]}$ 上是否存在点 $\text{[math]}$ ，使 $\text{[math]}$ 为等腰三角形？如果存在，请求出点 $\text{[math]}$ 的坐标；如果不存在，请说明理由.
答案解析收藏纠错 + 选题