一、选择题(本大题共有10个小题,每小题有且只有一个正确答案,每小题3分,共30分)
-
A .  B . ﹣
B . ﹣  C . 2
D . ﹣2
C . 2
D . ﹣2
-
A . ﹣2(a﹣b)=﹣2a﹣2b
B .  C .
C .  D .
D . 
-
-
4.
(2017八下·文安期末)
某班七个兴趣小组人数分别为4,4,5,x,6,6,7.已知这组数据的平均数是5,则这组数据的中位数是( )
A . 7
B . 6
C . 5
D . 4
-
A . 6
B . 7
C . ﹣6
D . ﹣7
-
6.
(2017·冷水滩模拟)
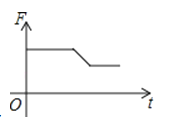
如图,挂在弹簧称上的长方体铁块浸没在水中,提着弹簧称匀速上移,直至铁块浮出水面停留在空中(不计空气阻力),弹簧称的读数F(N)与时间t(s)的函数图象大致是( )

-
A . 50°
B . 55°
C . 60°
D . 65°
-
A . m的最小值是1
B . m的最小值是﹣1
C . m的最大值是0
D . m的最大值是2
-
9.
(2016·石峰模拟)
矩形ABCD中,AB=2,AD=1,点M在边CD上,若AM平分∠DMB,则DM的长是( )

-
10.
(2016·石峰模拟)
如图,已知抛物线y=ax2+bx+c与轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1 , 则下列结论:
①b>0;②a﹣b+c<0;③阴影部分的面积为4;④若c=﹣1,则b2=4a.
正确的是( )

A . ①③
B . ②③
C . ②④
D . ③④
二、填空题(本大题共8小题,请将答案写在答题卡的相应位置上,每小题3分,满分24分)
-
-
-
-
-
15.
(2016·石峰模拟)
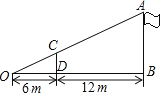
如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的顶端C、A与O点在一条直线上,则根据图中数据可得旗杆AB的高为m.
-
16.
(2016·石峰模拟)
把直线y=﹣x﹣3向上平移m个单位,与直线y=2x+4的交点在第二象限,则m的取值范围是
.
-
17.
(2017·西秀模拟)
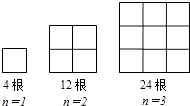
如图是由火柴棒搭成的几何图案,则第n个图案中有
根火柴棒.(用含n的代数式表示)
三、解答题(本大题共8个小题,请将解答过程写在答题卡相应的位置上,满分66分)
-
-
-
20.
(2016·石峰模拟)
为进一步推广“阳光体育”大课间活动,某中学对已开设的A实心球,B立定跳远,C跑步,D跳绳四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:
-
(1)
请计算本次调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整;
-
(2)
随机抽取了5名喜欢“跑步”的学生,其中有3名女生,2名男生,现从这5名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.

-
21.
(2016·石峰模拟)
我市校计划购买甲、乙两种树苗共200株来绿化校园,甲种树苗每株25元,乙种树苗每株30元,通过调查了解,甲乙两种树苗成活率分别是90%和95%.
-
(1)
若购买这种树苗共用去5600元,则甲、乙两种树苗各购买了多少株?
-
(2)
如果要求这200株树苗的成活率不低于93%,那么乙种树苗至少要购买多少株.
-
22.
(2016·石峰模拟)
如图,BD是△ABC的角平分线,点E,F分别在BC、AB上,且DE∥AB,EF∥AC.

-
-
(2)
若∠ABC=60°,BD=6,求四边形ADEF的面积.
-
23.
(2016·石峰模拟)
如图,正比例函数y=2x的图象与反比例函数y= k x 的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.

-
-
(2)
利用图象求出不等式2x>

的解集.
-
24.
(2016·石峰模拟)
如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.

-
-
(2)
试探究线段EF、OD、OP之间的等量关系,并加以证明;
-
(3)
若BC=6,tan∠F=

,求cos∠ACB的值和线段PE的长.
-
-
-
(2)
设抛物线与x轴两个交点为A(x1 , 0),B(x2 , 0),且x2>x1 , 若x2﹣x1=5,求c的值;
-
(3)
在(2)的条件下,设抛物线与y轴的交点为C,抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,求出点M的坐标;若不存在,请说明理由.
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C . 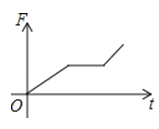 D .
D .