浙江省温州市绣山中学2020届九年级下学期数学第一次学业水平...

更新时间：2020-08-25 浏览次数：367 类型：中考模拟

一、选择题(本题有10小题，每小题4分，共40分.)

1. (2020·温州模拟) 计算2-3的结果是（）

A . -1 B . 0 C . 1 D . 5

答案解析收藏纠错 + 选题
2. (2020·温州模拟) 如图，由三个相同小立方体组成的几何图形的左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2020·温州模拟) 根据调查显示，温州市去年中考报名人数约83600人，83600用科学记数法可以表示为（）

A . 836×10² B . 83.6×10³ C . 8.36×10⁴ D . 0.836×10⁵

答案解析收藏纠错 + 选题
4. (2020·温州模拟) 在平面直角坐标系中，点P(-1，2)关于原点对称的点在（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
5. (2020·温州模拟) 方程 $\text{[math]}$ 的根是（）

A . x=3 B . x=2 C . x=-2 D . x=-2或x=3

答案解析收藏纠错 + 选题
6. (2020·温州模拟) 为调查某班学生每天使用零花钱的情况，张华随机调查了20名同学，结果如下表：

每天使用零花钱(单位：元)

10

15

20

25

30

人数

1

3

6

5

5

则这20名同学每天使用的零花钱的中位数是（）

A . 17.5元 B . 20元 C . 22.5元 D . 25元

答案解析收藏纠错 + 选题
7. (2020·温州模拟) 关于x的一元二次方程x²-2x+m=0有两个相等的实数根，则实数m的值为（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
8. (2023·鹿城模拟) 如图为一节楼梯的示意图，BC⊥AC，∠BAC=α，AC=6米。现要在楼梯上铺一块地毯，楼梯宽度为1米，则地毯的面积至少需要（）平方米。

A . 6tanα+6 B . $\text{[math]}$ +6 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020·温州模拟) 已知点A(x₁ ， y₁)，B(x₂ ， y₂)在二次函数y=x²-bx的图象上，当x₁ ， x₂满足2<x₁<x₂<3时，均有y₁<y₂<0，则b的值可以是（）

A . 2.1 B . 3.4 C . 4.5 D . 6

答案解析收藏纠错 + 选题
10. (2020·温州模拟) 在矩形ABCD中(AB<BC)，四边形ABFE为正方形，G，H分别是DE，CF的中点，将矩形DGHC移至FB右侧得到矩形FBKL，延长GH与KL交于点M，以K为圆心，KM为半径作圆弧与BH交于点P，古代印度利用这个方法，可以得到与矩形ABCD面积相等的正方形的边长。若矩形ABCD的面积为16，HP：PF=1：4，则CH的值为（）

A . $\text{[math]}$ B . 1 C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题

二、填空题(本题有6小题，每小题5分，共30分)

11. (2020·温州模拟) 因式分解：m²-6m+9= 。

答案解析收藏纠错 + 选题
12. (2024九下·温州模拟) 不等式组 $\text{[math]}$ 的解为。

答案解析收藏纠错 + 选题
13. (2020·温州模拟) 在一个不透明的布袋里装有2个黑球，1个白球，它们除颜色外都相同。小方从袋子中摸出一个球为白球的概率是。

答案解析收藏纠错 + 选题
14. (2023·鹿城模拟) 一个圆锥的侧面展开图是半径为8的半圆，则该圆锥的底面半径是。

答案解析收藏纠错 + 选题
15. (2020·温州模拟) 如图，点A，B分别在反比例函数y₁= $\text{[math]}$ (x>0)和y₂= $\text{[math]}$ (x<0)的图象上，线段AB与y轴正半轴交于点P。若P为AB中点，k₁-k₂=3，则△AOB的面积为。

答案解析收藏纠错 + 选题
16. (2020·温州模拟) 如图1是一盏可调节台灯，图2，图3为示意图，固定底座AO⊥OE于点O，AB为固定支撑杆，BC为可绕着点B旋转的调节杆，灯体CD始终保持垂直BC，MN为台灯照射在桌面的区域，如图2，旋转调节杆使BC∥OE，已知此时DM=DN，tan∠B= $\text{[math]}$ ，AO=CD=1dm，AB=5dm，BC=7dm，点M恰好为ON的中点，则cos∠DME的值为，如图3，旋转调节杆使BC⊥AB，则此时MN= dm。

答案解析收藏纠错 + 选题

三、解答题(本题有8小题，共80分)

17. (2020·温州模拟)
1. （1）计算：|-3|-4cos60°+(2019-2020)⁰。
2. （2）先化简，再求值：(x+2)²-x(x-2)，其中x=2。
答案解析收藏纠错 + 选题
18. (2020八下·通榆期末) 如图，方格纸中每个小方格的边长均为1个单位，请按要求画图。
1. （1）在图1中画出一个格点△ABC，使∠ABC=90°，且AB与BC的长度都是无理数。
2. （2）在图2中画出一个格点四边形ABCD，使AC⊥BD，且四边形的面积为5。
答案解析收藏纠错 + 选题
19. (2020·温州模拟) 如图，AB，DE交于点F，AD∥BE，点C在线段AB上，且AC=BE，AD=BC，连结CD，CE。
1. （1）求证：∠ADC=∠BCE。
2. （2）若∠A=40°，∠ADC=20°，求∠CDE的度数。
答案解析收藏纠错 + 选题
20. (2020·温州模拟) 某校开发了“摄影、绘画、器乐、书法”四门拓展课程。为了解全校学生对每门课程的选择情况，随机抽取了部分学生进行调查(每人必选且只能选一门)。现将调查结果绘制成如下两幅不完整的统计图：
1. （1）本次随机调查了名学生；补全条形统计图中的空缺部分(画图后请标注相应的数据)。
2. （2）求图2中“摄影”所对应的扇形的圆心角度数。
3. （3）若该校共有1800名学生，请估计全校学生选择“书法”课程的人数。
答案解析收藏纠错 + 选题
21. (2020·温州模拟) 如图，在△ACD中，∠D=90°，点O在AC上，以OC为半径的半圆O与AD相切于点E，与AC，CD分别交于点B，F，连结CE。
1. （1）求证：CE平分∠ACD。
2. （2）若AE=4，AB=2，求FC的长。
答案解析收藏纠错 + 选题
22. (2020·温州模拟) 如图，抛物线y=ax²+bx+c与x轴交于点A(-3m，0)，B(1，0)，与y轴交于点C(0，2m)(m>0)。
1. （1）当m=1时，求抛物线的表达式及对称轴。
2. （2） P为抛物线在第二象限上的一点，BP交对称轴于点D。若tan∠PBA= $\text{[math]}$ ，PD= $\text{[math]}$ DB，求m的值。
答案解析收藏纠错 + 选题
23. (2020·温州模拟) 疫情发生后，口罩成了人们生活的必需品.某药店销售A，B两种口罩，今年3月份的进价如下表：

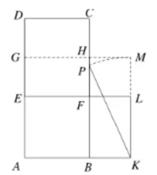
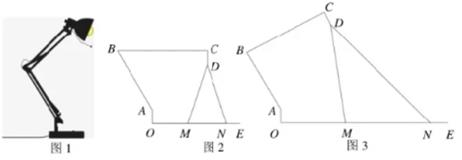
A种口罩

B种口罩

进价(元/包)

12

28

已知B种口罩每包售价比A种口罩贵20元，9包A种口罩和4包B种口罩总售价相同。
1. （1）求A种口罩和B种口罩每包售价。
2. （2）若该药店3月份购进A种和B种口罩共1500包进行销售，且B种口罩数量不超过A种口罩的 $\text{[math]}$ ，若所进口罩全部售出，则应该购进A种口罩多少包，才能使利润最大，并求出最大利润。
3. （3）为满足不同顾客的需求，该药店准备4月份新增购进进价为每包10元的C种口罩，A种和B种口罩仍按需购进，进价与3月份相同，A种口罩的数量是B种口罩的4倍，共花费12000元，则该店至少可以购进三种口罩共多少包？
答案解析收藏纠错 + 选题
24. (2020·温州模拟) 如图，在正方形ABCD中，AB=6，E为AC上一点，以AE为直角边构造等腰直角△AEF(点F在AB左侧)，分别延长FB，DE交于点H，DH交线段BC于点M，连结BE。
1. （1）求证：△AFB≌△AED
2. （2）当AE=4 $\text{[math]}$ 时，求tan∠MBH的值。
3. （3）当点H关于直线BE的对称点落在△ABC的边上时，求∠EBC的度数。
4. （4）若△BEH与△DEC的面积相等，记△EMC与△ABE的面积分别为S₁ ， S₂ ，则 $\text{[math]}$ 的值为。(直接写出答案)
答案解析收藏纠错 + 选题