吉林省长春市宽城区2020年中考数学二模试卷

更新时间：2024-07-13 浏览次数：325 类型：中考模拟

一、选择题

1. (2020·宽城模拟) -5的绝对值是（）

A . -5 B . 5 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020·宽城模拟) 预计到2025年，中国5G用户将超过460000000，将460000000这个数用科学记数法表示为（）

A . 0.46×10⁹ B . 4.6×10⁹ C . 4.6×10⁸ D . 46×10⁷

答案解析收藏纠错 + 选题
3. (2020·宽城模拟) 右图是由5个相同的小正方体组成的立体图形，这个立体图形的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2020·宽城模拟) 把不等式x+1≤2x-1的解集在数轴上表示，正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2020·宽城模拟) 关于x的一元二次方程x²+ax-1=0的根的情况是（）

A . 有两个不相等的实数根。 B . 有两个相等的实数根。 C . 只有一个实数根 D . 没有实数根

答案解析收藏纠错 + 选题
6. (2020·宽城模拟) 下表是小丽填写的实践活动报告的部分内容：

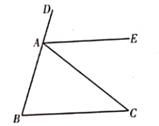
题目

测量树顶端到地面的高度

测量目标示意图

相关数据

AB=10m，α=45°，β=56°

设树顶端到地面的高度DC为xm，根据以上条件，下面所列方程正确的是（）

A . x=（x-10）cos56° B . x=（x-10）tan56° C . x-10=xcos56° D . x-10=xtan56°

答案解析收藏纠错 + 选题
7. (2020·宽城模拟) 如图，在Rt△ABC中，∠ACB=90°，分别以点B和点C为圆心、大于BC一半的长为半径作圆弧，两弧相交于点D和点E，作直线DE交AB于点F，交BC于点G，连结CF。若AC=3，CG=2，则CF的长为（）

A . 3.5 B . 3 C . 2.5 D . 2

答案解析收藏纠错 + 选题
8. (2020·宽城模拟) 如图，在平面直角坐标系中，点A、B的坐标分别为（-2，3）、（0，1），将线段AB沿x轴的正方向平移m（m>0）个单位，得到线段A' B'。若点A'、B'都落在函数y= $\text{[math]}$ （k≠0，x>0的图象上，则k的值为（）

A . 1 B . $\text{[math]}$ C . 3 D . 6

答案解析收藏纠错 + 选题

二、填空题

9. (2024·长春) 计算： $\text{[math]}$ - $\text{[math]}$ =

答案解析收藏纠错 + 选题
10. (2020·宽城模拟) 分解因式：x³-16x= 。

答案解析收藏纠错 + 选题
11. (2020·宽城模拟) 如图，点D是△ABC的边BA延长线上一点，AE∥BC。若∠DAC=110°，∠B=70°，则∠EAC的大小为度。

答案解析收藏纠错 + 选题
12. (2020·宽城模拟) 如图，小林的身高为1.8m，他在路灯下的影长为2m，小林距路灯杆底部为3m，则路灯灯泡距地面的高度为m。

答案解析收藏纠错 + 选题
13. (2020·宽城模拟) 如图，在平面直角坐标系中，直线y=-2x+4交x轴、y轴于A、B两点，将线段AB绕着点B逆时针方向旋转90°，点A落在点A'处，则点A'的坐标为。

答案解析收藏纠错 + 选题
14. (2019九上·宁都期中) 如图，小明的父亲在相距2米的两棵树间拴了一根绳子，给小明做了一个简易的秋千。拴绳子的地方距地面高都是2.5米，绳子自然下垂呈抛物线状，身高1米的小明距较近的那棵树0.5米时，头部刚好接触到绳子，则绳子的最低点距地面的距离为米。

答案解析收藏纠错 + 选题

三、解答题

15. (2020·宽城模拟) 以下是小鹏化简代数式（a-2）²+（a+1）（a-1）-2a（a-3）的过程。
解：原式=a²-2a+4+a²-1-2a²+6a……①

=（a²+a²-2a²）+（-2a+6a）+（4-1） ……②

=4a+3……③
1. （1）小鹏的化简过程在第步开始出错，错误的原因是。
2. （2）请你帮助小鹏写出正确的化简过程，并计算当a= $\text{[math]}$ 时代数式的值。
答案解析收藏纠错 + 选题
16. (2020·宽城模拟) 在一个不透明的盒子中装有三张卡片，分别标有数字1，2，5，这些卡片除数字不同外其余均相同．现从盒子中随机抽取一张卡片记下数字后放回，洗匀后再随机抽取一张卡片。用画树状图或列表的方法，求两次抽取的卡片上数字之和为偶数的概率。

答案解析收藏纠错 + 选题
17. (2020·宽城模拟) 供电局的电力维修工人要到30千米远的郊区进行电力抢修．维修工人骑摩托车先从供电局出发，15分钟后，抢修车装载着所需材料出发，沿着与维修工人相同的路线行驶，结果他们同时到达。已知抢修车的速度是摩托车速度的1.5倍，求摩托车的速度。

答案解析收藏纠错 + 选题
18. (2020·宽城模拟) 图①、图②均是5×4的正方形网格，每个小正方形的顶点称为格点。△ABC的顶点均在格点上，要求只用无刻度的直尺，分别按下列要求画图。
1. （1）在图①中画线段CD，满足CD⊥AB于点D。
2. （2）在图②中的线段AC上找到一点M，满足S_△ABC=4S_△BCM（保留确定点Ｍ的画图痕迹）。
答案解析收藏纠错 + 选题
19. (2020·宽城模拟) 如图，AB是⊙O的直径，BD、CD分别是过⊙O上点B、点C的切线，且∠BDC=110°，连结AC。
1. （1）求∠A的度数。
2. （2）若⊙O的直径为6，求 $\text{[math]}$ 的长。（结果保留）
答案解析收藏纠错 + 选题

20. (2020·宽城模拟) 第二十四届冬季奥林匹克运动会将于2022年在北京市和张家口市举行。为了调查学生对冬奥知识的了解情况，某校对七、八年级全体学生进行了相关知识测试，然后从七、八年级各随机抽取了20名学生的成绩（百分制），并对数据（成绩）进行了整理、描述和分析。下面给出了部分信息。

Ⅰ．七年级20名学生成绩的频数分布表如下：

七年级学生样本成绩频数分布表

成绩m（分）	频数（人数）
50≤m<60	1
60≤m<70	2
70≤m<80	3
80≤m<90	8
90≤m<100	6
合计	20

Ⅱ．七年级20名学生成绩在80≤m<90这一组的具体成绩是：

87 88 88 88 89 89 89 89

Ⅲ．七、八年级学生样本成绩的平均数、中位数、众数如下表所示：

	平均数	中位数	众数
七年级	84	n	89
八年级	84.2	85	85

根据以上提供的信息，解答下列问题：

（1））表中n的值为。
（2）在学生样本成绩中，某学生的成绩是87分，在他所属年级抽取的学生中排在前10名，根据表中数据判断该学生所在年级，并说明理由。
（3）七年级共有学生180名，若将不低于80分的成绩定为优秀，请估计七年级成绩优秀的学生人数。

答案解析收藏纠错 + 选题

21. (2020·宽城模拟) 李师傅驾车从甲地去乙地，途中在加油站加了一次油，加油时，车载电脑显示油箱中剩余油量为4升。已知汽车行驶时每小时的耗油量一定，设油箱中剩余油量为y（升），汽车行驶时间为x（时），y与x之间的函数图象如图所示。
1. （1）求李师傅加油前y与x之间的函数关系式。
2. （2）求a的值。
3. （3）求李师傅在加油站的加油量。
答案解析收藏纠错 + 选题
22. (2020·宽城模拟) 教材呈现：下图是华师版八年级下册数学教材第111页的部分内容。

问题解决：
1. （1）请结合图①，写出例1的完整解答过程。
2. （2）如图②，连结OE，则OE的长为。
3. （3）如图③，若点P是对角线BD上的一个动点，连结PC、PE，则PC+PE的最小值为。
答案解析收藏纠错 + 选题
23. (2020·宽城模拟) 如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，CD为斜边AB的中线。点P从点A出发，沿AB以每秒5个单位的速度向终点B运动。过点P作PE⊥AC于E，PF⊥BC于F，得到矩形PECF，CD与矩形PECF的一边交于点G，连结PC。设点P的运动时间为t秒。
1. （1）求线段CF的长。（用含t的代数式表示）
2. （2）当t= $\text{[math]}$ 时，求线段PG的长。
3. （3）当点P不与点A、B、D重合时，设矩形PECF与△PCD重叠部分图形的面积为S，求S与t之间的函数关系式。
4. （4）在点P出发的同时，点Q从点D出发，沿DC-CD以每秒6个单位的速度向终点D运动、当点Q在矩形PECF内部时，直接写出t的取值范围。
答案解析收藏纠错 + 选题
24. (2020·宽城模拟) 在平面直角坐标系中，已知函数y=- $\text{[math]}$ +nx+1（x≥0），其中n为常数。
1. （1）当n>0时，求这个函数图象的顶点坐标。（用含n的代数式表示）
2. （2）当y的最大值为1时，且|n|≤2，求整数n的值。
3. （3）当直线y=n+2与函数y=- $\text{[math]}$ +nx+1（x≥0）的图象只有一个公共点时，求n的取值范围。
4. （4）设点A在y轴上，点B在x轴的正半轴上，已知点A的坐标为（0，2n），以OA为边作正方形OACB。当函数y=- $\text{[math]}$ +nx+1（x≥0）的图象与正方形OACB的边有两个公共点时，直接写出n的取值范围。
答案解析收藏纠错 + 选题