河南省济源县2020年数学中考评价检测试卷（一）

更新时间：2020-06-11 浏览次数：220 类型：中考模拟

一、选择题

1. (2020·济源模拟) -7的绝对值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 7 D . -7

答案解析收藏纠错 + 选题
2. (2020·济源模拟) 最小的开花结果植物的果实质量只有0.000000076克，该数字用科学记数法表示为（）

A . 7.6×10⁹ B . 76×10^﹣9 C . 7.6×10^﹣9 D . 7.6×10^﹣8

答案解析收藏纠错 + 选题
3. (2021九上·紫金期末) 下面几何体的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2020·济源模拟) 下列各运算中，计算正确的是（）

A . $\text{[math]}$ B . （﹣2x²y）³=﹣8x⁵y³ C . （﹣5）⁰=0 D . a⁶÷a³=a²

答案解析收藏纠错 + 选题
5. 下列调查，应采用全面调查的是（）

A . 对我市七年级学生身高的调查 B . 对我国研制的“ $\text{[math]}$ ”大飞机零部件的调查 C . 对我市各乡镇猪肉价格的调查 D . 对我国“东风-41”洲际弹道导弹射程的调查

答案解析收藏纠错 + 选题
6. (2020·济源模拟) 《九章算术》中记录的一道题译为白话文是：把一份文件用慢马送到900里外的城市，需要的时间比规定时间多一天，如果用快马送，所需的吋间比规定时间少3天，已知快马的速度是慢马的2倍，求规定时间. 设规定时间为x天，则可列方程为（）.

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020九上·新余期末) 已知关于x的一元二次方程3x²+4x﹣5=0，下列说法正确的是（）

A . 方程有两个相等的实数根 B . 方程有两个不相等的实数根 C . 没有实数根 D . 无法确定

答案解析收藏纠错 + 选题
8. (2022·天桥模拟) 小明和小颖做“剪刀、石头、布”的游戏，假设他们每次出这三种手势的可能性相同，则在一次游戏中两人手势相同的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020·济源模拟) 如图，在△ABC中，按以下步骤作图：①分别以A、B为圆心，大于 $\text{[math]}$ AB的长为半径画弧，相交于两点M，N；②作直线MN交AC于点D，连接BD.若∠A＝25°，则∠CDB＝（）

A . 25° B . 90° C . 50° D . 60°

答案解析收藏纠错 + 选题
10. (2020·金华模拟) 如图，在一单位为1的方格纸上， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ …，都是斜边在 $\text{[math]}$ 轴上，斜边长分别为2，4，6，…的等腰直角三角形，若 $\text{[math]}$ 的顶点坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则依图中所示规律， $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2020·济源模拟) 计算（﹣ $\text{[math]}$ ）^﹣2﹣ $\text{[math]}$ +2cos30°＝.

答案解析收藏纠错 + 选题
12. (2020八下·烟台期末) 已知不等式组 $\text{[math]}$ 的解集为 $\text{[math]}$ ，则 $\text{[math]}$ 的值是.

答案解析收藏纠错 + 选题
13. (2020·济源模拟) 如图，正方形OABC的边长为2，以O为圆心，EF为直径的半圆经过点A，连接AE、CF相交于点P.将正方形OABC从OA与OF重合的位置开始，绕着点O逆时针旋转90°的过程中，线段OP的最小值为.

答案解析收藏纠错 + 选题
14. (2020·济源模拟) 如图，在扇形AOB中，∠AOB=90°，正方形CDEF的顶点C是 $\text{[math]}$ 的中点，点D在OB上，点E在OB的延长线上，当正方形CDEF的边长为2 $\text{[math]}$ 时，阴影部分的面积为

答案解析收藏纠错 + 选题
15. (2020·济源模拟) 如图：△ABC是等边三角形，AB＝12，E是AC中点，D是直线BC上一动点，线段ED绕点E逆时针旋转90°，得线段EF，当点D运动时，则线段AF的最小值为.

答案解析收藏纠错 + 选题

三、解答题

16. (2020·沈阳模拟) 先化简，再求值：（2﹣ $\text{[math]}$ ）÷ $\text{[math]}$ ，其中x＝ $\text{[math]}$ ﹣3.

答案解析收藏纠错 + 选题

17. (2020·济源模拟) 重庆一中开展了“爱生活•爱运动”的活动，以鼓励学生积极参与体育锻炼.为了解学生每周体育锻炼时间，学校在活动之前对八年级同学进行了抽样调査，并根据调査结果将学生每周的体育锻炼时间分为3小时、4小时、5小时、6小时、7小时共五种情况.小明根据调查结构制作了如图两幅统计图，请你结合图中所给信息解答下列问题：

（整理数据）

“爱生活•爱运动”的活动结束之后，再次抽查这部分学生的体育锻炼时间：

一周体育锻炼时间（小时）	3	4	5	6	7
人数	3	5	15	a	10

活动之后部分学生体育锻炼时间的统计表

（分析数据）

	平均数	中位数	众数
活动之前锻炼时间（小时）	5	5	5
活动之后锻炼时间（小时）	5.52	b	c

请根据调查信息分析：

（1）补全条形统计图，并计算a＝，b＝小时，c＝小时；
（2）小亮同学在活动之前与活动之后的这两次调查中，体育锻炼时间均为5小时，根据体育锻炼时间由多到少进行排名统计，请问他在被调查同学中体育锻炼时间排名靠前的是（填“活动之前”或“活动之后”），理由是；
（3）已知八年级共2200名学生，请估算全年级学生在活动结束后，每周体育锻炼时间至少有6小时的学生人数有多少人？

答案解析收藏纠错 + 选题

18. (2021九上·榆林期中) 如图，直线y₁=3x﹣5与反比例函数y₂= $\text{[math]}$ 的图象相交A（2，m），B（n，﹣6）两点，连接OA，OB.
1. （1）求k和n的值；
2. （2）求△AOB的面积；
3. （3）直接写出y₁＞y₂时自变量x的取值范围.
答案解析收藏纠错 + 选题
19. (2020·济源模拟) 如图，AB＝BC，以BC为直径作⊙O，AC交⊙O于点E，过点E作EG⊥AB于点F，交CB的延长线于点G.
1. （1）求证：EG是⊙O的切线；
2. （2）若GF＝2 $\text{[math]}$ ，GB＝4，求⊙O的半径.
答案解析收藏纠错 + 选题
20. (2020·济源模拟) 如图，小巷左右两侧是竖直的墙，一架梯子AC斜靠在右墙，测得梯子与地面的夹角为45°，梯子底端与墙的距离CB＝2米，若梯子底端C的位置不动，再将梯子斜靠在左墙，测得梯子与地面的夹角为60°，则此时梯子的顶端与地面的距离A'D的长是多少米？（结果保留根号）

答案解析收藏纠错 + 选题
21. (2019八上·西安期中) 甲、乙两人相约周末登花果山，甲、乙两人距地面的高度y（米）与登山时间x（分）之间的函数图象如图所示，根据图象所提供的信息解答下列问题：
1. （1）甲登山上升的速度是每分钟米，乙在A地时距地面的高度b为米．
2. （2）若乙提速后，乙的登山上升速度是甲登山上升速度的3倍，请求出乙登山全程中，距地面的高度y（米）与登山时间x（分）之间的函数关系式．
3. （3）登山多长时间时，甲、乙两人距地面的高度差为50米？
答案解析收藏纠错 + 选题
22. (2020·济源模拟) 如图，正方形ABCD的边长为4，点E，F分别在边AB，AD上，且∠ECF＝45°，CF的延长线交BA的延长线于点G，CE的延长线交DA的延长线于点H，连接AC，EF．，GH．
1. （1）填空：∠AHC∠ACG；（填“＞”或“＜”或“＝”）
2. （2）线段AC，AG，AH什么关系？请说明理由；
3. （3）设AE＝m，
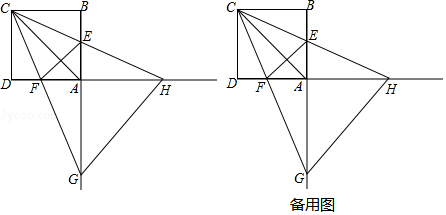
  ①△AGH的面积S有变化吗？如果变化．请求出S与m的函数关系式；如果不变化，请求出定值．
  
  ②请直接写出使△CGH是等腰三角形的m值．
答案解析收藏纠错 + 选题
23. (2020·济源模拟) 已知抛物线y＝x²+（2m﹣1）x﹣2m（m＞0.5）的最低点的纵坐标为﹣4.
1. （1）求抛物线的解析式；
2. （2）如图1，抛物线与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，D为抛物线上的一点，BD平分四边形ABCD的面积，求点D的坐标；
3. （3）如图2，平移抛物线y＝x²+（2m﹣1）x﹣2m，使其顶点为坐标原点，直线y＝﹣2上有一动点P，过点P作两条直线，分别与抛物线有唯一的公共点E、F（直线PE、PF不与y轴平行），求证：直线EF恒过某一定点.
答案解析收藏纠错 + 选题