江苏省无锡市滨湖区2020年数学中考一模试卷

更新时间：2020-07-09 浏览次数：277 类型：中考模拟

一、选择题

1. (2023七下·宽城期末) 8的立方根为（）

A . 2 B . ±2 C . －2 D . 4

答案解析收藏纠错 + 选题
2. (2020·滨湖模拟) 方程（x＋1）（x－3）=－4的解是（）

A . x₁=－1，x₂=3 B . x₁=1，x₂=0 C . x₁=1，x₂=－1 D . x₁=x₂=1

答案解析收藏纠错 + 选题
3. (2020·滨湖模拟) 若2x=3y，且x≠0，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2020·滨湖模拟) 若一次函数y=2x＋m的图像与x轴相交于点A（－3，0），则m的值为（）

A . －3 B . 6 C . －6 D . 6或－6

答案解析收藏纠错 + 选题
5. (2020·滨湖模拟) 下列调查方式不合适的是（）

A . 为了了解某班学生今年“五一”期间每天的锻炼时间，采用普查的方式进行统计 B . 小芳的妈妈在炒菜时为了了解菜的咸淡情况，采用抽样的方式品尝一下 C . 在防控新冠肺炎疫情的关键时期，敬老院门卫处对来访人员的体温情况采用抽样的方式进行检测 D . 为了了解江苏省中小学生寒假期间每天登陆“省名师空中课堂”进行学习的情况，采用抽样的方式进行调查

答案解析收藏纠错 + 选题
6. (2020·滨湖模拟) 若四边形ABCD为菱形，则下列结论中不一定成立的是（）

A . AC=BD B . AC⊥BD C . AB∥CD D . AB=CD

答案解析收藏纠错 + 选题
7. (2020·滨湖模拟) 如图为一个正方体的表面展开图，在这个正方体中P、Q、R这三个面所对的面上的数字分别为（）

A . 2，3，4 B . 3，2，4 C . 3，4，2 D . 以上都不正确

答案解析收藏纠错 + 选题
8. (2020·滨湖模拟) 如图，已知C为 $\text{[math]}$ 上一点，若∠AOB=100°，则∠ACB的度数为（）

A . 50° B . 80° C . 100° D . 130°

答案解析收藏纠错 + 选题
9. (2020·滨湖模拟) 如图，在△ABC中，AC=6，∠BAC=60°，AM为△ABC的角平分线，若 $\text{[math]}$ ，则AM长为（）

A . 6 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2020七上·江都期中) 当n≥2时，设1＋2＋3＋…＋n的末位数字为a_n ，比如1＋2=3，末位数字为3，故a₂=3，又如1＋2＋3＋4=10，末位数字为0，故a₄=0，则a₂＋a₃＋…＋a₈₈₈的末位数字为（）

A . 0 B . 5 C . 6 D . 9

答案解析收藏纠错 + 选题

二、填空题

11. (2024六下·长宁期中) ﹣ $\text{[math]}$ 的倒数是．

答案解析收藏纠错 + 选题
12. (2020·滨湖模拟) 我区约有2930名学生参加本次模拟考试，这个数据用科学记数法可以表示为.
（精确到百位）

答案解析收藏纠错 + 选题
13. (2020·滨湖模拟) 分解因式：2x²﹣18=．

答案解析收藏纠错 + 选题
14. (2020·滨湖模拟) 请写出任意一个经过第一、二、四象限的一次函数解析式：.

答案解析收藏纠错 + 选题
15. (2023九上·石家庄期中) 若一个直角三角形的两条直角边长分别为7cm和24cm，则这个三角形的外接圆的直径长为cm.

答案解析收藏纠错 + 选题
16. (2020·滨湖模拟) 给出如下5种图形：①矩形，②等边三角形，③正五边形，④圆，⑤线段.其中，是轴对称图形但不是中心对称图形的有.（请将所有符合题意的序号填在横线上）

答案解析收藏纠错 + 选题
17. (2020九上·高新月考) 如图，已知⊙O的半径为3cm，点A、B、C把⊙O三等分，分别以OA、OB、OC为直径作圆，则图中阴影部分的面积为.

答案解析收藏纠错 + 选题
18. (2020·滨湖模拟) 如图，已知A、B两点都在反比例函数y= $\text{[math]}$ 位于第二象限部分的图象上，且△OAB为等边三角形，若AB=6，则k的值为.

答案解析收藏纠错 + 选题

三、解答题

19. (2020·滨湖模拟)
1. （1）计算： $\text{[math]}$ ；
2. （2）化简：（2x＋5）²－（2x＋3）（2x－3）.
答案解析收藏纠错 + 选题
20. (2020·滨湖模拟)
1. （1）解方程： $\text{[math]}$ － $\text{[math]}$ =1；
2. （2）解不等式组： $\text{[math]}$
答案解析收藏纠错 + 选题
21. (2020·滨湖模拟) 如图是由若干个完全相同的小正方形构成的纸片，请你剪2刀，将它拼接成一个新的正方形.请在图中用粗实线画出剪的位置，并简要表述你的拼接方式.

答案解析收藏纠错 + 选题
22. (2024八上·长兴期末) 如图，在△ABC中，∠ABC的平分线与AC的垂直平分线相交于点D，过点D作DF⊥BC，DG⊥AB，垂足分别为F、G.
1. （1）求证：AG=CF；
2. （2）若BG=5，AC=6，求△ABC的周长.
答案解析收藏纠错 + 选题

23. (2020·滨湖模拟) 受疫情影响，某地无法按原计划正常开学.在延迟开学期间该地区组织了在线教学活动.开学后，某校针对各班在线教学的个性化落实情况，通过初评决定从甲、乙、丙三个班中推荐一个作为在线教学先进班级，下表是这三个班的五项指标的考评得分表（单位：分）：

班级	课程设置	课程质量	在线答疑	作业情况	学生满意度
甲班	10	10	6	10	7
乙班	10	8	8	9	8
丙班	9	10	8	7	9

根据统计表中的信息解答下列问题：

（1） ①请确定如下的“五项指标的考评得分分析表”中的a、b、c的值：

班级	平均分	众数	中位数
甲班	8.6	10	a
乙班	8.6	b	8
丙班	c	9	9

②甲、乙、丙三个班在线教学活动“学生满意度”考评度考评得分的极差为分.

（2）如果学校把“课程设置”、“课程质量”、“在线答疑”、“作业情况”、“学生满意度”这五项指标得分按照2∶2∶3∶1∶2的比例确定最终成绩，请你通过计算判断应推荐哪个班为在线教学先进班级？

答案解析收藏纠错 + 选题

24. (2020·滨湖模拟) 在平面直角坐标系中，已知A（1，0）、B（1，2）、C（3，4）、D（3，2）.若在这四点中任取两点，设M为连接这两点所得线段的中点，请用画树状图法或列表法求出点M在一次函数y=2x－1的图象上的概率.

答案解析收藏纠错 + 选题
25. (2020·滨湖模拟) 一方有难，八方支援.已知甲、乙两地急需一批物资，其中甲地需要240吨，乙地需要260吨.A、B两城市通过募捐，很快筹集齐了这种物资，其中A城市筹到物资200吨，B城市筹到物资300吨.已知从A、B两城市将每吨物资分别运往甲、乙两地所需运费成本（单位：元/吨）如表所示.问：怎样调运可使总运费最少？最少运费为多少元？

答案解析收藏纠错 + 选题
26. (2020·滨湖模拟) 如图，已知AB为半圆O的直径，P为半圆上的一个动点（不含端点），以OP、OB为一组邻边作▱POBQ，连接OQ、AP，设OQ、AP的中点分别为M、N，连接PM、ON.
1. （1）试判断四边形OMPN的形状，并说明理由.
2. （2）若点P从点B出发，以每秒15°的速度，绕点O在半圆上逆时针方向运动，设运动时间为ts.
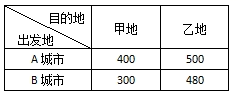
  ①试求：当t为何值时，四边形OMPN的面积取得最大值？并判断此时直线PQ与半圆O的位置关系（需说明理由）；
  
  ②是否存在这样的t，使得点Q落在半圆O内？若存在，请直接写出t的取值范围；若不存在，请说明理由.
答案解析收藏纠错 + 选题
27. (2020·滨湖模拟) 如图，已知二次函数y=x²－mx－m－1的图象交x轴于A、B两点（A、B分别位于坐标原点O的左、右两侧），交y轴于点C，且△ABC的面积为6.
1. （1）求这个二次函数的表达式；
2. （2）若P为平面内一点，且PB=3PA，试求当△PAB的面积取得最大值时点P的坐标，并求此时直线PO将△ABC分成的两部分的面积之比.
答案解析收藏纠错 + 选题
28. (2020·滨湖模拟) 阅读材料：等腰三角形具有性质“等边对等角”．事实上，不等边三角形也具有类似性质“大边对大角”，如图1，在△ABC中，如果AB＞AC，那么∠ACB＞∠ABC．证明如下：将AB沿△ABC的角平分线AD翻折（如图2），因为AB＞AC，所以点B落在AC的延长线上的点B′处．于是，由∠ACB＞∠B′，∠ABC＝∠B′，可得∠ACB＞∠ABC．
1. （1）灵活运用：从上面的证法可以看出，折纸常常能为证明一个命题提供思路和方法．由此小明想到可用类似方法证明“大角对大边”，如图3，在△ABC中，如果∠ACB＞∠ABC，那么AB＞AC．小明的思路是：沿BC的垂直平分线翻折……请你帮助小明完成后面的证明过程．
2. （2）拓展延伸：请运用上述方法或结论解决如下问题：
  如图4，已知M为正方形ABCD的边CD上一点（不含端点），连接AM并延长，交BC的延长线于点N．求证：AM＋AN＞2BD．
答案解析收藏纠错 + 选题