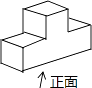
 B .
B . 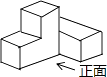 C .
C .  D .
D . 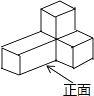
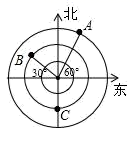
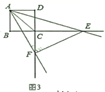
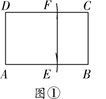
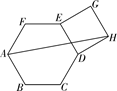
甲:以点A为圆心,AD长为半径画弧,交AB于点E,以点D为圆心,AD长为半径画弧,交CD于点F,连接EF,则四边形AEFD即为所求;
乙:作∠DAB的平分线,交CD于点M,同理作∠ADC的平分线,交AB于点N,连接MN,则四边形ADMN即为所求.
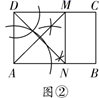
对于以上两种作法,可以做出的判定是( )
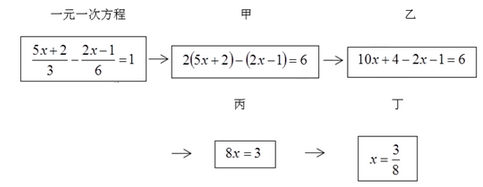
接力中,自己负责的一步出现错误的是( )
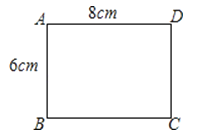


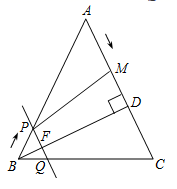
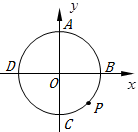
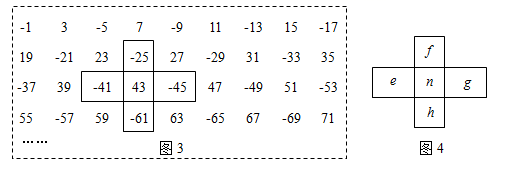
⑴连结 ,当
时,则点
的横坐标是.
⑵连结 ,设线段
的长为
,则
的取值范围是.
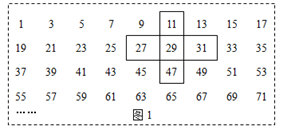
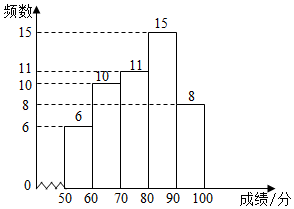
a.七年级成绩频数分布直方图:
b.七年级成绩在 这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
| 年级 | 平均数 | 中位数 |
| 七 | 76.9 | m |
| 八 | 79.2 | 79.5 |
根据以上信息,回答下列问题: