广西南宁市2020年初中毕业班第一次适应性模拟测试数学试卷

更新时间：2020-07-11 浏览次数：309 类型：中考模拟

一、选择题(本大题共12小题，每小题3分，共36分，在每小题给出的四个选项中只有一项是符合要求的，请用2B铅笔把答题卡上对应题目的答案标号涂黑.)

1. (2020七下·延平期中) -3的相反数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 3 D . -3

答案解析收藏纠错 + 选题
2. (2022·普洱模拟) 如图是某几何体的三视图，该几何体是（）

A . 圆柱 B . 正方体 C . 圆锥 D . 球

答案解析收藏纠错 + 选题
3. (2020·南宁模拟) 计算(a²b)³的结果是（）

A . a²b³ B . a⁵b³ C . a⁶b D . a⁶b³

答案解析收藏纠错 + 选题
4. (2020·汝南模拟) 如图，DE∥BC，BE平分∠ABC，若∠1=70°，则∠CBE的度数为（）

A . 20° B . 35° C . 55° D . 70°

答案解析收藏纠错 + 选题
5. (2020·南宁模拟) 若分式 $\text{[math]}$ 有意义，则x的取值范围是（）

A . x>2 B . x≠2 C . x≠0 D . x≠-2

答案解析收藏纠错 + 选题
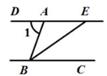
6. (2020八上·嘉兴月考) 如图，已知在△ABC中，AB=AC，AB=5，BC=3，以A，B两点为圆心，大于 $\text{[math]}$ AB的长为半径画弧，两弧相交于点M，N，连接MN与AC相交于点D，则△BDC的周长为（）

A . 8 B . 10 C . 11 D . 13

答案解析收藏纠错 + 选题
7. (2024七下·牟平期末) 中国清代算书《御制数理精蕴》中有这样一题：“马四匹、牛六头，共价四十八两(我国古代货币单位)；马三匹、牛五头，共价三十八两．问马、牛各价几何?”设马每匹 $\text{[math]}$ 两，牛每头 $\text{[math]}$ 两，根据题意可列方程组为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020·南宁模拟) 如果圆锥的底面半径为3，母线长为6，那么它的侧面积等于（）

A . 9π B . 18π C . 24π D . 36π

答案解析收藏纠错 + 选题
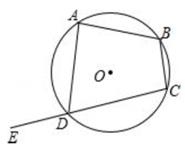
9. (2020·南宁模拟) 如图，四边形ABCD内接于⊙O，E为CD延长线上一点，若∠ADE=110°，则∠B=（）

A . 80° B . 100° C . 110° D . 120°

答案解析收藏纠错 + 选题
10. (2020·南宁模拟) 现有A，B，C，D，E五个同学，他们分别来自一中，二中，三中，已知： (1)每所学校至少有他们中的一名学生；(2)在二中联欢会上，A，B，E作为被邀请的客人演奏了小提琴；(3)B过去曾在三中学习，后来转学了，现在同D在同一个班学习；(4)D，E是同一所学校的三好学生.根据以上叙述可以断定A所在的学校为（）

A . 三中 B . 二中 C . 一中 D . 不确定

答案解析收藏纠错 + 选题
11. (2020·南宁模拟) 如图，在平面直角坐标系中，Rt△ABC的顶点A，C的坐标分别是(0，3)，(3、0)。∠ACB=90°，AC=2BC，若函数y= $\text{[math]}$ (k>0，x>0)的图象经过点B，则k的值为（）

A . $\text{[math]}$ B . 9 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
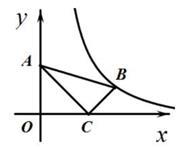
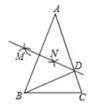
12. (2020·南宁模拟) 如图，以矩形ABCD对角线AC为底边作等腰直角△ACE，连接BE，分别交AD，AC于点F，N，CD=AF，AM平分∠BAN。下列结论：

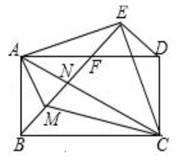
①△CDE≌△AFE；②∠BCM=∠NCM；③AE·AM=NE·FM；④BN²+EF²=EN²；其中正确结论的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题

二、填空题(本大题共6小题，每小题3分，共18分。)

13. (2020·南宁模拟) 不等式2x+1≤5的解集是。

答案解析收藏纠错 + 选题
14. (2020·南宁模拟) 科技不断发展，晶体管长度越造越短，长度只有0.000000006米的晶体管已经诞生，该数用科学记数法表示为米。

答案解析收藏纠错 + 选题
15. (2022九上·河东期末) 不透明袋子中装有7个球，其中有2个红球、3个绿球和2个蓝球，这些球除颜色外无其他差别．从袋子中随机取出1个球，则它是绿球的概率是．

答案解析收藏纠错 + 选题
16. (2020·南宁模拟) 如图，AC是⊙O的内接正六边形的一边，点B在 $\text{[math]}$ 上，且BC是⊙O的内接正十边形的一边，若AB是⊙O的内接正n边形的一边，则n=。

答案解析收藏纠错 + 选题
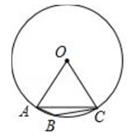
17. (2020·南宁模拟) 如图，某海防哨所O发现在它的西北方向，距离哨所400米的A处有一艘船向正东方向航行，航行一段时间后到达哨所北偏东60°方向的B处，则此时这艘船与哨所的距离OB约为米。(精确到1米，参考数据： $\text{[math]}$ ≈1.414， $\text{[math]}$ ≈1.732)

答案解析收藏纠错 + 选题
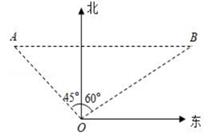
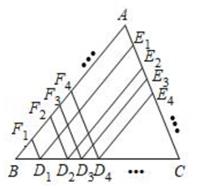
18. (2020·南宁模拟) 如图，在△ABC中，AB=5，AC=4，若进行以下操作，边BC上从左到右依次取点D₁ ， D₂ ， D₃ ， D₄.…；过点D₁作AB，AC的平行线分别交AC，AB于点E₁ ， F₁；过点D₂作AB，AC的平行线分别交AC，AB于点E₂ ， F₂；过点D₃作AB，AC的平行线分别交AC，AB于点E₃ ， F₃…，则4(D₁E₁+D₂E₂+…+D₂₀₂₀E₂₀₂₀)+5(D₁F₁+D₂F₂+…+D₂₀₂₀F₂₀₂₀)=。

答案解析收藏纠错 + 选题

三、解答题(本大题共8小题，共66分，解答应写出文字说明，证明过程或演算步骤)

19. (2020·南宁模拟) 计算：(-1)²+[4-(1+ $\text{[math]}$ )×2]

答案解析收藏纠错 + 选题
20. (2020·南宁模拟) 解分式方程： $\text{[math]}$

答案解析收藏纠错 + 选题
21. (2020·南宁模拟) 在下面的网格中，每个小正方形的边长均为1，△ABC的三个顶点都是网格线的交点，已知B，C两点的坐标分别为(-3，0)，(-1，-1)。
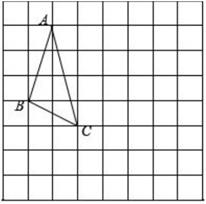
1. （1） ①请在图中画出平面直角坐标系，并直接写出点A的坐标。
  ②将△ABC绕着坐标原点顺时针旋转90°，画出旋转后的△A'B'C'。
2. （2）求△A'B'C'的面积。
答案解析收藏纠错 + 选题

22. (2020·南宁模拟) 2020年寒假期间，由于新冠肺炎疫情的爆发，檀华中学开展“停课不停学”的线上学习活动.学校教务处为了解九年级学生网上学习的情况，从该校九年级随机抽取20名学生，进行了每天网上学习的调查.数据如下(单位：时)

3	2.5	0.6	1	2	2	2	3.3	2.5	1.8
2.5	2.2	3.5	4	1.5	2.5	3.1	2.8	3.3	2.4

整理数据：

网上学习时间x(时)	0<x≤1	1<x≤2	2<x≤3	3<x≤4
人数	2	5	8	5

分析数据：

统计量	平均数	中位数	众数
数值	2.4	m	n

根据以上信息，解答下列问题：

（1）上表中的中位数m的值为，众数n的值为。
（2）用样本中的平均数估计该校九年级学生平均每人一个月(按30天计算)网上学习的时间。
（3）已知该校九年级学生有500名，估计每天网上学习时间超过2小时的学生人数。

答案解析收藏纠错 + 选题

23. (2020·南宁模拟) 如图，在△ABC中，AD=BD=CD，E是AD的中点，过点A作AF∥BC交BE的延长线于点F，连接CF。
1. （1）求证：△AEF≌△DEB；
2. （2）求证：四边形A DCF是菱形。
答案解析收藏纠错 + 选题
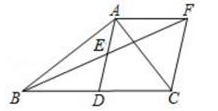
24. (2020·南宁模拟) 某校的李，黄两位老师同住一小区，该小区与学校相距2400米。李老师从小区步行去学校，出发21分钟后黄老师再出发，黄老师从小区先骑公共一行车，途经学校又骑行若干米到达还车点后，立即跑步回学校。已知黄老师跑步的速度比李老师步行的速度每分钟快40米。设李老师步行的时间为x(分)，图1中线段OA和折线B—C—D分别表示李老师、黄老师离开小区的路程y(米)与李老师步行时间x(分)的函数关系的图象；图2表示李、黄两位老师之间的距离s(米)与李老师步行时间x(分)的函数关系的图象(不完整)。
根据图1和图2中所给信息，解答下列问题：
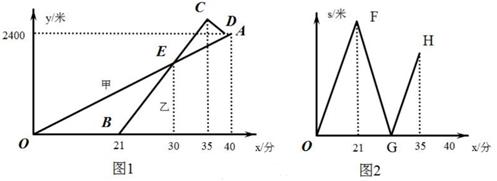
1. （1）求李老师步行的平均速度和黄老师出发时李老师离开小区的路程；
2. （2）求黄老师骑自行车的速度和黄老师到达还车点时李，黄老师之间的距离；
3. （3）在图2中，求黄老师到达学校时与李老师的距离并画出当35≤x≤40时s关于x的函数的大致图象，请标明关键点的坐标。(温馨提示：请画在答题卷相对应的图上)
答案解析收藏纠错 + 选题
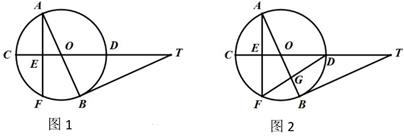
25. (2020·南宁模拟) 如图1所示，已知AB，CD是OD的直径，T是CD延长线的一点，⊙O的弦AF交CD于点E，且AE=EF，OA²=OE·OT。
1. （1）如图1，求证：BT是⊙O的切线；
2. （2）在图1中连接CB，DB，若 $\text{[math]}$ ，求tanT的值；
3. （3）如图2，连接DF交AB于点G，若BT=6 $\text{[math]}$ ，DT=6。求DG的长。
答案解析收藏纠错 + 选题
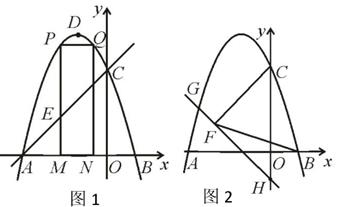
26. (2020·南宁模拟) 如图，抛物线y=ax²+2ax+c的图象与x轴交于A，B两点(点A在点B的左边)AB=4，与y轴交于点C，OC=OA，点D为抛物线的顶点。
1. （1）求抛物线的解析式；
2. （2）点M(m，0)为线段AB上一点(点M不与点A，B重合)，过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N，可得矩形PQNM，如图1，点P在点Q左边，当矩形PQNM的周长最大时，求m的值，并求出此时的△AEM的面积；
3. （3）如图2，已知H(0，-1)，点G在抛物线上，连HG，直线HG⊥CF，足为F，若BF=BC，求点G的坐标。
答案解析收藏纠错 + 选题