浙江省嘉兴市南湖区2020年数学中考一模试卷

更新时间：2024-07-13 浏览次数：567 类型：中考模拟

一、选择题(本题有10小题，每小题3分，共30分．请选出各题中唯一的正确选项，不选、多选、错选，均不给分)

1. (2020·南湖模拟) 下列各组数中，互为相反数的是（）

A . 4与-4 B . $\text{[math]}$ 与4 C . 4与 $\text{[math]}$ D . -4与 $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020·南湖模拟) 下列图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（）

A . 赵爽弦图 B . 笛卡尔心形线 C . 科克曲线 D . 斐波那契螺旋线

答案解析收藏纠错 + 选题
3. (2020·南湖模拟) 下列运算正确的是（）

A . a+a=a² B . x²．x³=x⁵ C . (a+1)²=a²+1 D . (2x)³=6x³

答案解析收藏纠错 + 选题
4. (2020·南湖模拟) 有10位同学参加歌唱比赛，成绩各不相同，按成绩取前5位进入决赛，一位选手知道了自己的成绩后，要判断能否进入决赛，则他还需知道这10位同学成绩的（）

A . 平均数 B . 中位数 C . 方差 D . 众数

答案解析收藏纠错 + 选题
5. (2024七下·庐江期中) 已知正方形的面积为50，则该正方形的边长介于（）

A . 6与7之间 B . 7与8之间 C . 8与9之间 D . 9与10之间

答案解析收藏纠错 + 选题
6. (2020·南湖模拟) 车队运送一批货物．若每车装4吨，剩下8吨未装；若每车装5吨，则剩余1辆车。甲、乙两人设该车队有x辆车，丙、丁两人设这批货物有y吨，分别列出如下方程：
甲：4x+8=5(x-1)；乙：4x-8=5(x+1)；丙： $\text{[math]}$ +1；丁： $\text{[math]}$ -1。
其中所列方程正确的是（）

A . 甲、丙 B . 甲、丁 C . 乙、丙 D . 乙、丁

答案解析收藏纠错 + 选题
7. (2020·南湖模拟) 图1是一张圆形纸片，直径AB=4，现将点A折叠至圆心O形成折痕CD，再把点C，D都折叠至圆心O处，最后将图形打开铺平(如图2所示)，则弧EF的长为（）

A . $\text{[math]}$ π B . $\text{[math]}$ π C . $\text{[math]}$ π D . $\text{[math]}$ π

答案解析收藏纠错 + 选题
8. (2020·南湖模拟) 已知抛物线y=ax²+bx+c(u>0)交x轴于点A(x₁ ， 0)，B(x₂ ， 0)，且x₁<x₂ ，点P(m，n)(n<0)在该抛物线上．下列四个判断：①b²-4ac≥0；②若a+c=b+3，则该抛物线一定经过点(1，3)；③方程a²+bx+c=n的解是x=m；④当m= $\text{[math]}$
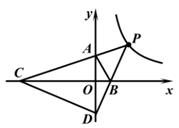
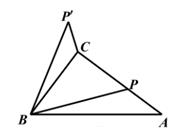
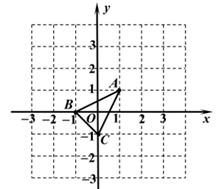
时，△PAB的面积最大。其中判断一定正确的序号是（）

A . ① B . ② C . ③ D . ④

答案解析收藏纠错 + 选题
9. (2020·南湖模拟) 如图所示的一个大长方形，它被分割成4个大小不同的正方形①，②，③，④和一个小长方形⑤，若已知大长方形的周长，则一定能计算出周长的图形是（）

A . ②③ B . ④⑤ C . ②④ D . ③⑤

答案解析收藏纠错 + 选题
10. (2020·南湖模拟) 如图，平面直角坐标系中，O为原点，点A，B分别在y轴、x轴的正半轴上，△AOB的两条外角平分线交于点P，且点P在反比例函数y= $\text{[math]}$ 的图象上。PA，PB的延长线分别交x轴、y轴于点C，D，连结CD，则△OCD的面积是（）

A . 8 B . 8 $\text{[math]}$ C . 16 D . 16 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题(本题有6小题，每小题4分，共24分)

11. (2024七上·龙湾期中) 8的立方根是．

答案解析收藏纠错 + 选题
12. (2020·南湖模拟) 已知y是x的函数，且当x>0时，y随x的增大而减小．则这个函数的表达式可以是。(写出一个符合题意的答案即可)

答案解析收藏纠错 + 选题
13. (2020·南湖模拟) 方程组： $\text{[math]}$ 的解是。

答案解析收藏纠错 + 选题
14. (2020·南湖模拟) 如图是2020年2月17一23日浙江省“新冠肺炎”每日出院人数折线统计图，相邻两日间日出院人数增长有快慢，其中最大的增长率是。(精确到0.1%)

答案解析收藏纠错 + 选题
15. (2020·南湖模拟) 对于实数a，b，c，定义mid{a，b，c}=b(a≥b≥c)。例如mid{-1，1，3}=1；mid{1，2，2}=2，若1≤mid{1，a-1，a+1}≤2，则a的取值范围是。

答案解析收藏纠错 + 选题
16. (2020·南湖模拟) 如图，在△ABC中，∠ACB=90°，AB=10，BC=6，P是边AC上的动点，将线段BP绕点B按逆时针方向旋转到BP'，旋转角等于∠ABC，连结CP'。
1. （1）当P'，C，P在一条直线上时，线段AP的长是。
2. （2）线段CP'的最小值是。
答案解析收藏纠错 + 选题

三、解答题(本题有8小题，第17~19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分)

17. (2020·南湖模拟)
1. （1）计算： $\text{[math]}$
2. （2）化简： $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2020·南湖模拟) 如图，在平面直角坐标系中，△ABC的各顶点坐标为A(1，1)，B(-1，0)，C(0，-1)。
1. （1）以坐标原点O为位似中心，在图中作出△ABC的一个位似图形△A'B'C'，使它与△ABC的位似比为2。
2. （2）在(1)的条件下，求 $\text{[math]}$ 的值。
答案解析收藏纠错 + 选题
19. (2023九上·新昌期中) 一个不透明的口袋中有三个完全相同的小球，球上分别标有数字-1，1，2，第一次从袋中任意摸出一个小球(不放回)，得到的数字作为点Ｍ的横坐标x；再从袋中余下的两个小球中任意摸出一个小球，得到的数字作为点Ｍ的纵坐标y。
1. （1）用列表法或画树状图法，列出点M(x，y)的所有可能结果。
2. （2）求点M(x，y)在反比例函数y= $\text{[math]}$ 的图象上的概率。
答案解析收藏纠错 + 选题
20. (2020·南湖模拟) 如图，在菱形ABCD中，∠A=60°，经过点C且半径为2的⊙O分别切AB，AD于点B，D。
1. （1）求 $\text{[math]}$ 的度数。
2. （2）求图中阴影部分的面积。
答案解析收藏纠错 + 选题
21. (2020·南湖模拟) 温度的计量，世界上大部分国家都使用摄氏温度(℃)，但美、英等国的天气预报仍然使用华氏温度(°F)．已知两种计量之间的关系是我们已学的某种函数，且两种计量的部分对应值如下表。

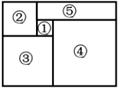
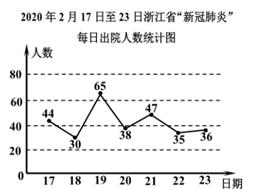
摄氏C(℃)

0

10

20

30

40

50

华氏F(°F)

32

50

68

86

104

122
1. （1）判断华氏F(°F)与摄氏C(℃)之间是何种函数关系？并求出F(°F)关于C(℃)的函数表达式。
2. （2）求华氏为0°F时的摄氏温度。
3. （3）华氏温度的值与对应的摄氏温度的值能否相等？若能，求相等的值；若不能，请说明理由。
答案解析收藏纠错 + 选题
22. (2020·南湖模拟) 如图1是一款“雷达式”懒人椅。当懒人椅完全展开时，其侧面示意图如图2所示，金属杆AB，CD在点O处连接，且分别与金属杆EF在点B，D处连接，金属杆CD的OD部分可以伸缩(即OD的长度可变)．已知0A=50cm，OB=20cm，OC=30cm，DE=BF=5cm．当把懒人椅完全叠合时，金属杆AB，CD，EF重合在一条直线上(如图3所示)，此时点E和点A重合。
1. （1）如图2，已知∠BOD=6∠ODB，∠OBF=140°。
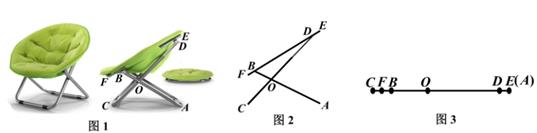
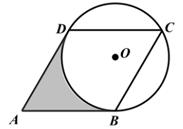
  ①求∠AOC的度数。
  
  ②求点A，C之间的距离。
2. （2）如图3，当懒人椅完全叠合时，求CF与CD的长。
答案解析收藏纠错 + 选题
23. (2020·南湖模拟) 在平面直角坐标系中，P，Q是抛物线y=ax²(a>0)上不重合的两点，点Ｍ(0，2)，直线PM，QM的比例系数互为相反数。
1. （1）若点P的坐标为(2，8)，求α的值。
2. （2）在(1)的条件下，求点Q的坐标。
3. （3）若点P，Q都在第一象限内，且点P的横坐标是点Ｑ的横坐标的3倍，试探究点P与点Q的纵坐标的差是否为定值？若是，求出该定值；若不是，请说明理由。
答案解析收藏纠错 + 选题
24. (2020·南湖模拟) 【方法提炼】
解答几何问题常常需要添辅助线，其中平移图形是重要的添辅助线策略．
【问题情境】
如图1，在正方形ABCD中，E，F，G分别是BC，AB，CD上的点，FG⊥AE于点Q。求证：AE=FG。
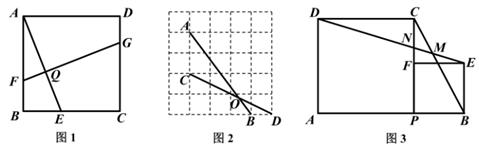
小明在分析解题思路时想到了两种平移法：
方法1：平移线段FG使点F与点B重合，构造全等三角形。
方法2：平移线段BC使点B与点F重合，构造全等三角形。
1. （1）【尝试应用】
  请按照小明的思路，选择其中一种方法进行证明．
2. （2）如图2，正方形网格中，点A，B，C，D为格点，AB交CD于点O，求tan∠AOC的值。
3. （3）如图3，点P是线段AB上的动点，分别以AP，BP为边在AB的同侧作正方形APCD与正方形PBEF，连结DE分别交线段BC，PC于点M，N。
  ①求∠DMC的度数。
  ②连结AC交DE于点H，求 $\text{[math]}$ 的值。
答案解析收藏纠错 + 选题