浙江省衢州市常山县2020年数学中考模拟试卷

更新时间：2020-08-07 浏览次数：266 类型：中考模拟

一、选择题（本题共10小题，每题3分，共30分）

1. (2020·常山模拟) 计算-1+2的值是（）

A . -1 B . 1 C . -3 D . 3

答案解析收藏纠错 + 选题
2. (2020·常山模拟) 常山三衢石林是国家4A级旅游景区，占地面积约为27600000平方米，数据27600000用科学记数法表示为（）

A . 0.276×10⁸ B . 2.76×10⁷ C . 2.76×10⁸ D . 27.6×10⁶

答案解析收藏纠错 + 选题
3. (2020·常山模拟) 下列计算正确的是（）

A . a³·a²=a⁵ B . a³÷a=a³ C . （a²）³=a⁵ D . （3a）³=3a³

答案解析收藏纠错 + 选题
4. (2020·常山模拟) 已知在Rt△ABC中，∠C=90°，AB=5，AC=3，则tanA的值（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020·常山模拟) 计算 $\text{[math]}$ 的结果为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . -1 D . 2

答案解析收藏纠错 + 选题
6. (2020·常山模拟) 不等式组 $\text{[math]}$ 的解在数轴上表示为（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2020·常山模拟) 甲、乙、丙、丁四人进行射击测试，成绩的平均数和方差如下表所示：

平均数

8.9

8.7

8.6

8.9

方差

2.5

5.5

2.5

6.5

根据表中数据，要从中选一名成绩好又发挥稳定的选手参加比赛，则应该选择（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
8. (2020·常山模拟) 如图，已知∠ACB=∠DBC，添加以下条件，不能判定△ABC≌△DCB的是（）

A . ∠ABC=∠DCB B . ∠A=∠D C . AC=DB D . AB=DC

答案解析收藏纠错 + 选题
9. (2020九上·湖州月考) 如图，⊙O的直径AB=10，CD是⊙O的弦，CD⊥AB，垂足为E，且BE：AE=1：4，则CD的长为（）

A . 10 B . 12 C . 8 D . 9

答案解析收藏纠错 + 选题
10. (2020·常山模拟) 如图1，一只蚂蚁从点O出发，以1厘米/秒速度沿着扇形AOB的边缘爬行一周。设爬行时间为x秒，蚂蚁到点O的距离为y厘米，y关于x的函数图象如图2所示，则扇形的面积为（）

A . 3 B . 6 C . $\text{[math]}$ π D . π

答案解析收藏纠错 + 选题

二、填空题（本题共6小题，每题4分，共24分）

11. (2020·常山模拟) 分解因式：a²-4a=。

答案解析收藏纠错 + 选题
12. (2020·常山模拟) 已知样本数据0，1，3，1，5，则这组数据的中位数是。

答案解析收藏纠错 + 选题
13. (2020七下·宁波期中) 已知 $\text{[math]}$ ，则3a+b的值是。

答案解析收藏纠错 + 选题

14. (2020·常山模拟) 已知二次函数y=ax²+bx+c自变量x的部分取值和对应函数值y如下表，则二次函数图象的对称轴是直线。

x	…	-4	-3	-1	1	2	3	…
y	…	21	13	3	1	3	7	…

答案解析收藏纠错 + 选题

15. (2020·常山模拟) 如图，在平面直角坐标系中，边长为2的正方形ABCD的顶点A与原点O重合，顶点B在直线l：y= $\text{[math]}$ x上，将正方形沿射线OB方向无滑动地翻滚.当正方形翻滚2020次点A对应点的坐标是。

答案解析收藏纠错 + 选题
16. (2020·常山模拟) 如图，反比例函数y= $\text{[math]}$ （k>0）图象经过Rt△OAB直角边AB的中点C，与斜边OB相交于点D，过点D作DE⊥y轴于点E，连结CO，CD。
1. （1） △ODE与△OAB的面积比为；
2. （2）若△COD的面积为1，则k的值为。
答案解析收藏纠错 + 选题

三、解答题（本题共有8小题，第17~19小题每小题6分，第20~21小题每小题8分，第22~23小题每小题10分，第24小题12分，共66分，请务必写出解答过程）

17. (2020·常山模拟) 计算： $\text{[math]}$ +（ $\text{[math]}$ ）^-1-2tan45°+（2-π）⁰

答案解析收藏纠错 + 选题
18. (2020·常山模拟) 已知：如图，点A，F，E，C在同一条直线上，AB∥CD，且AB=CD，AE=CF。求证：四边形BEDF是平行四边形。

答案解析收藏纠错 + 选题
19. (2020·常山模拟) 如图所示的直棱柱，其侧棱长为3cm，底面是边长为2cm的等边三角形。
1. （1）用尺规作图法补充完整它的三视图（保留作图痕迹，不要求写作法）。
2. （2）求该直棱柱左视图的面积。
答案解析收藏纠错 + 选题

20. (2020·常山模拟) 新冠肺炎疫情在全球蔓延，截止2020年5月14日，我国确诊病例达84464例，为了解新冠肺炎的易感人群是否与年龄相关，从中随机抽取50名确诊病例，对其年龄进行统计，制成如下不完整频数表和频数直方图。

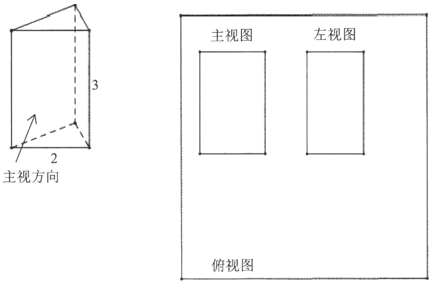
50名确诊病例年龄频数表

年龄段（岁）	频数
0≤x<20	1
20≤x<40	12
40≤x<60	a
60≤x<80	15
80≤x<100	2

根据图表解决下列问题：

（1）求表中a的值并补全频数直方图；
（2）从以上图表中写出两条相关的结论；
（3）小林、小敏响应社区号召，积极参加疫情联防联控工作，参与小区卡点值勤。某小区有A、B、C三个卡点，他们都可以从这三个卡点中任选一个参与值勤，求两人在同一卡点值勤的概率是多少（要求用列表法或画树状图求解）？

答案解析收藏纠错 + 选题

21. (2020·常山模拟) 如图，在Rt△ABC中，∠C=90°，∠ABC的平分线交AC于点D，点O是AB上一点，⊙O过B、D两点，且分别交AB、BC于点E、F。
1. （1）求证：AC是⊙O的切线；
2. （2）已知AB=6，BC=3，求 $\text{[math]}$ 的长。
答案解析收藏纠错 + 选题
22. (2020·常山模拟) 定义：有一组对角是直角，且夹其中一个直角的两边相等的四边形称为垂等四边形。
1. （1）在矩形，菱形，正方形中，一定是垂等四边形的是。
2. （2）如图，在垂等四边形ABCD中，∠ABC=∠ADC=90°，AD=CD，对角线AC与BD相交于点O。
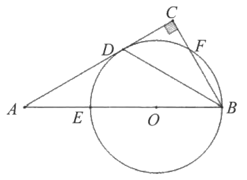
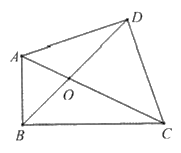
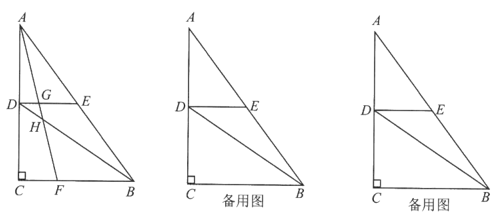
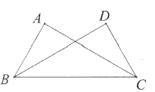
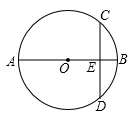
  ①求证：BD平分∠ABC；
  
  ②若AB=2，BC=4，求BD的长。
答案解析收藏纠错 + 选题
23. (2020·常山模拟) 常山是“胡柚之乡”，小明经过市场调查发现，某乡柚农家中胡柚每月的销售量与售价关系如下表：

售价x（元/箱）

80

90

100

110

…

月销量y（箱）

240

220

200

180

…

已知每箱胡柚的成本40元，设每箱胡柚的售价为x元。
1. （1）每箱胡柚的销售利润是元（请用含x的式子表示）；
2. （2）求月销量y与售价x的函数关系式；
3. （3）设销售胡柚的月利润为W元，那么每箱胡柚的售价为多少元时，当月的销售利润最大？最大利润是多少元？
答案解析收藏纠错 + 选题
24. (2020·常山模拟) 如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，DE是△ABC的中位线，点F是BC边上的一个动点，连结AF交BD于点H，交DE于点G。
1. （1）求△BDE的面积；
2. （2）当四边形DCFH与四边形BEGH的面积相等时，求 $\text{[math]}$ 的值；
3. （3）以点F为圆心，FB为半径作⊙F，当 $\text{[math]}$ 的值满足什么条件时，⊙F与线段DE有且只有一个交点。
答案解析收藏纠错 + 选题