一、选择题：本大题有10个小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项最符合题目要求。
-
A . 1至1.5之间
B . 1.5至2之间
C . 2至2.5之间
D . 2.5至3之间
-
-
3.
(2020·萧山模拟)
一组数据1，2，3，4，4，10，去掉10，剩下的数据和原数据相比，不变的是（ ）
A . 平均数
B . 中位数
C . 众数
D . 平均数和众数
-
A . x+1<0
B . x-1<0
C . 
<-1
D . -2x<10
-
5.
(2020·萧山模拟)
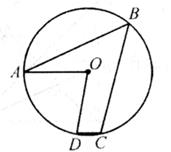
如图，A，B，C，D是⊙O上的点，∠AOD=80°，AO∥DC，则∠B的度数为（ ）
A . 40°
B . 45°
C . 50°
D . 55°
-
6.
(2020·萧山模拟)
某影院昨天甲、乙两种电影票共售出203张，甲票售出x张，每张35元，乙票每张20元，票房总额y，则（ ）
A . 15x-y+4060=0
B . x-15y+4060=0
C . 15x+y+4060=0
D . x-15y-4060=0
-
7.
(2020·萧山模拟)
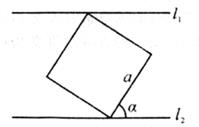
如图是墙壁上在l
1 ， l
2两条平行线间的边长为a的正方形瓷砖，该瓷砖与平行线的较大夹角为α，则两条平行线间的距离为（ ）
A . 2asinα
B . asinα+acosα
C . 2acosα
D . asinα-acosα
-
8.
(2020·萧山模拟)
如图，将直角三角形纸片ABC(∠A=90°，AB>AC)沿过点A的直线折叠，使得AC落在AB边上折痕为AD，展开纸片(如图①)；再次折叠该三角形纸片，使点A和点D重合，折痕为EF，展平纸片后得到△AEF(如图②)。若AC=6，AB=8，则折痕EF的长为（ ）
-
9.
(2020·萧山模拟)
已知二次函数y=ax²+bx+c，当x=2时，该函数取最大值8，设该函数图象与x轴的一个交点横坐标为x
1 ， 若x
1>4，则a的取值范围是（ ）
A . -3<a<-1
B . -2<a<0
C . -1<a<1
D . 2<a<4
-
10.
(2020·萧山模拟)
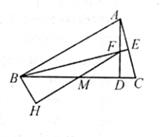
如图，△ABC中，AB=BC，AD⊥BC于点D，BE⊥AC于点E，交AD于点F，点Ｍ是BC的中点，连接FM并延长交AB的垂线BH于点H。下列说法中错误的是（ ）
A . 若∠ABC=30°，则DF+BH= 
BD
B . 若∠ABC=45°，则DF+BH=BD
C . 若∠ABC=60°(点Ｍ与点D重合)，则DF+BH= 
BD
D . 若∠ABC=90°(点B与点D重合)，则DF+BH=BD
二、填空题：本题有6个小题，每小题4分，共24分.
-
-
-
13.
(2022九上·齐齐哈尔月考)
一个不透明的袋子中装有四个小球，它们除了分别标有的数字1，2，3，6不同外，其他完全相同，任意从袋子中摸出一球后不放回，再任意摸出一球，则两次摸出的球所标数字之积为6的概率是
。
-
-
15.
(2020·萧山模拟)
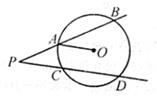
如图，射线PB，PD分别交⊙O于点A，B和点C，D，且AB=CD=8。已知⊙O半径等于5，OA∥PC，则OP的长度为
。
-
16.
(2020·萧山模拟)
若直线y=x+m与函数y=|x
2-2x-3|的图象只有一个交点，则交点坐标为
；若直线y=x+m与函数y=|x²-2x-3|的图象有四个公共点，则m的取值范围是
。
三、解答题：本题有7小题，共66分.解答应写出文字说明、证明过程或演算步骤。
-
-
18.
(2020·萧山模拟)
如图，
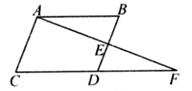
ABCD中，E为BC边上的中点，连AE并与DC的延长线交于点F。
求证：DC=CF。
-
19.
(2020九上·萧山开学考)
某校鼓励师生利用课余时间广泛阅读.为了解学生课外阅读情况，抽样调查了部分学生每周用于课外阅读的时间，过程如下：
数据收集：从全校随机抽取20名学生，进行了每周用于课外阅读时间的调查，数据如下(单位：min)
|
30
|
60
|
81
|
50
|
40
|
110
|
130
|
146
|
90
|
100
|
|
60
|
81
|
120
|
140
|
70
|
81
|
10
|
20
|
100
|
81
|
分段整理样本数据：
|
课外阅读时间x(min)
|
0≤x<40
|
40≤x<80
|
80≤x<120
|
120≤x<160
|
|
等级
|
D
|
C
|
B
|
A
|
|
人数
|
3
|
①
|
8
|
②
|
统计量：
得出结论：
-
-
（2）
如果该校现有学生400人，估计等级为“B”的学生有多少名？
-
（3）
假设平均阅读一本课外书的时间为160分钟，请你选择样本中的一种统计量估计该校学生每人一年(按52周计算)平均阅读多少本课外书？
-
20.
(2020·萧山模拟)
已知点A(x
1 ， y
1)，B(x
2 ， y
2)是反比例函数y=
(k≠0)图象上两点。
-
（1）
若点A，B关于原点中心对称，求5x1y2-7x2y1的值(则用含k的代数式表示)。
-
（2）
设x1=a-1，x2=a+1，若y1<y2 ， 求a的取值范围。
-
21.
(2020·萧山模拟)
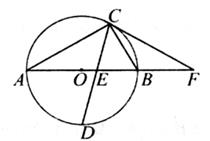
如图，AB是⊙O的直径，点C是圆上一点，点D是半圆的中点，连接CD交OB于点E，点F是AB延长线上一点，CF=EF。
-
-
（2）
若CF=5，tanA=
，求⊙O半径的长。
-
-
（1）
求证：函数y1=kx²+(2k-1)x-2的图象与x轴有交点。
-
（2）
已知函数y
1的图象与x轴的两个交点间的距离等于3，
①试求此时k的值。
②若y1>y2 ， 试求x的取值范围。
-
23.
(2020·萧山模拟)
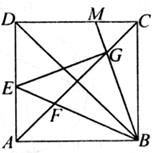
如图，在边长为6的正方形ABCD中，点E为边AD上的一个动点(与点A，D不重合) ，∠EBM=45°，BE交对角线AC于点F，BM交于AC于点G，交CD于点M。
-
-
（2）
设AE=x，S
△BEG=y，
①求y关于x的函数表达式及x的取值范围。
②当图中点E，M关于对角线BD成轴对称时，求y的值。
B . 
C . 
D . 
