河南省南阳市卧龙区2020年数学中考一模试卷

更新时间：2024-07-13 浏览次数：266 类型：中考模拟

一、选择题

1. (2020·卧龙模拟) $\text{[math]}$ 的绝对值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020·卧龙模拟) 预计到2025年，中国5G用户将达到460000000.将460000000科学记数法表示成a×10ⁿ（1≤a＜10，n是整数）的形式，则n的值应为（）

A . 9 B . 8 C . 7 D . 6

答案解析收藏纠错 + 选题
3. (2020·卧龙模拟) 如图，由四个正方体组成的几何体的左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2020·卧龙模拟) 下列计算：① $\text{[math]}$ ；②（x﹣2y）²＝x²﹣4y²；③（﹣a）⁴•a³＝﹣a⁷；④x¹⁰÷x⁵＝x² ，其中错误的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
5. (2020·卧龙模拟) 给定一组数据，那么这组数据的（）可以有多个.

A . 平均数 B . 中位数 C . 方差 D . 众数

答案解析收藏纠错 + 选题
6. (2020七下·唐河期中) 不等式组 $\text{[math]}$ 的解集在数轴上表示正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2020·卧龙模拟) 若关于x的一元二次方程x²+4x+k＝0有两个不相等的实数根，则k的取值范围是（）

A . k＜4 B . k＞4 C . k＜1 D . k＞1

答案解析收藏纠错 + 选题
8. (2023九下·佛山月考) 学校决定从甲、乙、丙三名学生中随机抽取两名介绍学习经验，则同时抽到乙、丙两名同学的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020·卧龙模拟) 如图，已知∠1＝39°，∠2＝39°，∠3＝54°，则∠4的度数是（）

A . 39° B . 51° C . 54° D . 126°

答案解析收藏纠错 + 选题
10. (2020·卧龙模拟) 如图，已知点A₁（1，1），将点A₁向上平移1个单位长度，再向右平移2个单位长度得到点A₂；将点A₂向上平移2个单位长度，再向右平移4个单位长度得到点A₃；将点A₃向上平移4个单位长度，再向右平移8个单位长度得到点A₄ ， …按这个规律平移下去得到点A_n（n为正整数），则点A_n的坐标是（）

A . （2ⁿ ， 2ⁿ^﹣¹） B . （2ⁿ^﹣¹ ， 2n） C . （2ⁿ^﹣¹ ， 2ⁿ+1） D . （2ⁿ﹣1，2ⁿ^﹣¹）

答案解析收藏纠错 + 选题

二、填空题

11. (2020·卧龙模拟) 计算：（ $\text{[math]}$ ﹣1）⁰﹣（ $\text{[math]}$ ）^﹣¹＝.

答案解析收藏纠错 + 选题
12. (2021九上·无棣期中) 已知抛物线y＝x²+mx+9的顶点在x轴上，则m的值为.

答案解析收藏纠错 + 选题
13. (2020·卧龙模拟) 如图，直线y=- $\text{[math]}$ x+4与 x轴、y轴的交点为A，B.按以下步骤作图：
①以点 A 为圆心，适当长度为半径作弧，分别交 AB，x 轴于点 C，D；

②分别以点 C，D 为圆心，大于 $\text{[math]}$ CD的长为半径作弧，两弧在∠OAB内交于点M；③作射线AM，交 y 轴于点E.则点 E 的坐标为

答案解析收藏纠错 + 选题
14. (2020·卧龙模拟) 如图，在扇形AOB中，∠AOB＝90°，点C在 $\text{[math]}$ ， $\text{[math]}$ ，OA＝3，CD⊥OB于点D，则图中阴影部分的面积为.

答案解析收藏纠错 + 选题
15. (2021·肇源模拟) 如图，在边长为3的等边△ABC中，点D在AC上，且CD＝1，点E在AB上（不与点A、B重合），连接DE，把△ADE沿DE折叠，当点A的对应点F落在等边△ABC的边上时，AE的长为.

答案解析收藏纠错 + 选题

三、解答题

16. (2020·卧龙模拟) 先化简，再求值：（ $\text{[math]}$ ﹣2）÷ $\text{[math]}$ ，其中x＝ $\text{[math]}$ ﹣1.

答案解析收藏纠错 + 选题

17. (2020·卧龙模拟) 某学校为了解九年级男同学1000米跑步的成绩，随机抽取了部分男生进行测试，并将测试成绩分为A、B、C、D四个等级，绘制了不完整的成绩等级频数表和扇形统计图.

成绩等级	频数
A	24
B	10
C	b
D	2
合计	a

（1）表中a＝，b＝；
（2）扇形图中C的圆心角度数是；
（3）若该校共有九年级男生600人，请估计没有获得A等级的学生人数.

答案解析收藏纠错 + 选题

18. (2020九上·南京月考) 已知△ABC内接于⊙O，AB是⊙O的直径，OD∥AC，AD＝OC.
1. （1）求证：四边形OCAD是平行四边形；
2. （2）若AD与⊙O相切，求∠B.
答案解析收藏纠错 + 选题
19. (2020·卧龙模拟) 如图，某海监船向正西方向航行，在A处望见一艘正在作业的渔船D在南偏西45°方向，海监船航行到B处时，望见渔船D在南偏东45°方向，又航行半小时到达C处望见渔船D在南偏东62°方向，若海监船的速度为40海里/小时，求A、B之间的距离.（精确到0.1海里，参考数据：sin62°≈0.88，cos62°≈0.47，tan62°≈1.88）

答案解析收藏纠错 + 选题

20. (2020·卧龙模拟) 某兴趣小组对函数y＝ $\text{[math]}$ 的图象和性质进行探究，请你帮助解决下面问题：

（1）函数y＝ $\text{[math]}$ 中自变量x的取值范围是；

（2）如表是x、y的几组对应值，则m＝；

x	…	﹣2	﹣1	0	1	2	4	5	6	7	8	…
y	…	$\text{[math]}$	m	$\text{[math]}$	0	﹣1	3	2	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	…

（3）如图，已经画出了该函数图象的一部分，请你画出函数图象的另一部分；
（4）该函数图象两个分支关于一个点成中心对称，这个点的坐标是；
（5）若函数y＝ $\text{[math]}$ 的图象上有三点A（x₁ ， y₁）、B（x₂ ， y₂）、C（x₃ ， y₃）且x₁＜x₂＜3＜x₃ ，则y₁、y₂、y₃的大小关系是（用“＜”连接）.

答案解析收藏纠错 + 选题

21. (2020·卧龙模拟) 在2020年新冠肺炎疫情期间，我市某企业为支援湖北，准备将购买的70吨蔬菜运往武汉，现有甲、乙两种货车可以租用，已知2辆甲货车和3辆乙货车一次可运44吨蔬菜；3辆甲货车和1辆乙货车一次可运38吨蔬菜.
1. （1）求每辆甲种货车和每辆乙种货车一次分别能运多少吨蔬菜？
2. （2）已知甲种货车每辆租金500元，乙种货车每辆租金450元，该企业共租用甲、乙两种货车8辆，设租甲种货车a辆，求租车总费用w（元）与a之间的函数关系式，并求出自变量a的取值范围；
3. （3）在（2）的条件下，请你为该企业设计出费用最少的方案，并求出最少的租车费用.
答案解析收藏纠错 + 选题
22. (2020·卧龙模拟) 在△ABC中，AC＝BC，∠ACB＝α，点D为直线BC上一动点，过点D作DF∥AC交直线AB于点F，将AD绕点D顺时针旋转α得到ED，ED交直线AB于点O，连接BE.
1. （1）问题发现：
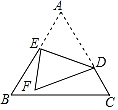
  如图1，α＝90°，点D在边BC上，猜想：
  
  ①AF与BE的数量关系是
  
  ②∠ABE＝度.
2. （2）拓展探究：
  如图2，0°＜α＜90°，点D在边BC上，请判断AF与BE的数量关系及∠ABE的度数，并给予证明.
3. （3）解决问题
  如图3，90°＜α＜180°，点D在射线BC上，且BD＝3CD，若AB＝8，请直接写出BE的长.
答案解析收藏纠错 + 选题
23. (2020·卧龙模拟) 如图，抛物线y＝ax²+bx+c（a＜0）与x轴交于点A（﹣2，0）、B（4，0），与y轴交于点C，且OC＝2OA.
1. （1）该抛物线的解析式为；
2. （2）直线y＝kx+l（k＞0）与y轴交于点D，与直线BC交于点M，与抛物线上直线BC上方部分交于点P，设m＝ $\text{[math]}$ ，求m的最大值及此时点P的坐标；
3. （3）若点D、P为（2）中求出的点，点Q为x轴的一个动点，点N为坐标平面内一点，当以点P、D、Q、N为顶点的四边形为矩形时，直接写出点N的坐标.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

河南省南阳市卧龙区2020年数学中考一模试卷

副标题：

*注意事项：

河南省南阳市卧龙区2020年数学中考一模试卷

试题分析

总体分析

题量分析

难度分析

知识点分析