辽宁省沈阳市和平区2020年数学中考二模试卷

更新时间：2020-08-25 浏览次数：241 类型：中考模拟

一、选择题

1. (2024八下·琼海期末) 地球平均半径约等于6 400 000米，6 400 000用科学记数法表示为（）

A . 64×10⁵ B . 6.4×10⁵ C . 6.4×10⁶ D . 6.4×10⁷

答案解析收藏纠错 + 选题
2. (2020·和平模拟) 面积为3的正方形的边长范围在（）

A . 0和1之间 B . 1和2之间 C . 2和3之间 D . 3和4之间

答案解析收藏纠错 + 选题
3. (2023八下·雅安期末) 某几何体的三视图如图所示，该几何体是（）

A . 圆锥 B . 圆柱 C . 三棱锥 D . 球

答案解析收藏纠错 + 选题
4. (2020七下·连山期末) 不等式﹣x+3≥0的正整数解有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
5. (2020·和平模拟) 一次函数y=﹣x﹣2的图象经过（）

A . 第一、二、三象限 B . 第一、二、四象限 C . 第一、三，四象限 D . 第二、三、四象限

答案解析收藏纠错 + 选题
6. (2020·和平模拟) 下列运算正确的是（）

A . m²+m²＝2m² B . （m﹣n）（n﹣m）＝n²﹣m² C . （﹣2mn）²＝﹣4m²n² D . （2m）³÷m³＝2

答案解析收藏纠错 + 选题
7. (2020·和平模拟) 下列四种基本尺规作图分别表示：①作一个角等于已知角；②作一个角的平分线；③过直线外一点作已知直线的垂线；④作一条线段的垂直平分线，则对应作法错误的是（）

A . ① B . ② C . ③ D . ④

答案解析收藏纠错 + 选题
8. (2020·和平模拟) 将一副三角板如图叠放，则图中∠α余角的度数为（）

A . 15° B . 75° C . 85° D . 165°

答案解析收藏纠错 + 选题
9. (2020·和平模拟) 某校组建了书法、音乐、美术、舞蹈、演讲5个社团，随机调查了部分学生.被调查学生每人都参加且只参加了其中一个社团活动，并将调查结果制成了如图两幅不完整的统计图，在扇形统计图中，“音乐”所对应的扇形圆心角度数是（）度.

A . 25% B . 25 C . 60 D . 90

答案解析收藏纠错 + 选题
10. (2020·和平模拟) 如图，已知l₁∥l₂∥l₃∥l₄ ，相邻两条平行直线间的距离相等.若等腰直角 $\text{[math]}$ 的三个顶点分别在三条平行直线上，则∠α的正弦值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2024七下·南海月考) 正方形是轴对称图形，它共有条对称轴．

答案解析收藏纠错 + 选题
12. (2024八下·海门月考) 面试时，某人的基础知识、表达能力、工作态度的得分分别是80分、70分、90分，若依次按照30%、30%、40%的比例确定面试成绩，则这个人的面试成绩是分.

答案解析收藏纠错 + 选题
13. (2024九下·江门模拟) 化简： $\text{[math]}$ =．

答案解析收藏纠错 + 选题
14. (2020·和平模拟) 如图，在△ABC中，AB＝AC，AD是△ABC的一条角平分线，若AB＝13.AD＝12.则BC的长为.

答案解析收藏纠错 + 选题
15. (2023八下·娄底期中) 如图，菱形ABCD中，对角线AC与BD相交于点O，且AC=8，BD=6，则菱形ABCD的高DH=．

答案解析收藏纠错 + 选题
16. (2020·和平模拟) 如图，在正方形ABCD中，AB＝16.连接AC，点P在线段AC上，PA＝ $\text{[math]}$ AC，作射线PM与边AB相交于点E.将射线PM绕点P逆时针旋转90°得到射线PN，射线PN与边BC相交于点F.当△AEP的面积为 $\text{[math]}$ 时.在边CD上取一点G.则△AFG周长的最小值是.

答案解析收藏纠错 + 选题

三、解答题

17. (2020·和平模拟) 计算：|1﹣6cos30°|﹣ $\text{[math]}$ +（﹣ $\text{[math]}$ ）^﹣²﹣（﹣3）⁰.

答案解析收藏纠错 + 选题
18. (2020·和平模拟) 一个不透明的盒子中装有两个红球和一个蓝球.这些球除颜色外都相同.
1. （1）从中随机摸出一个球.记下颜色后放回.再从中随机摸出一个球.
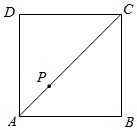
  ①请用列表法或树状图法，求第一次摸到蓝球，第二次摸到红球的概率；
  
  ②请直接写出两次摸到的球的颜色能配成紫色的概率 ▲ .
2. （2）从中随机摸出一个球，记下颜色后不放回.再从中随机摸出一个球，请直接写出两次摸到的球的颜色能配成紫色的概率.
答案解析收藏纠错 + 选题
19. (2020·和平模拟) 如图，▱ABCD中，∠A＝45°，连接BD，且BD⊥AD，点E、点F分别是AB、CD上的点，连接EF交BD于点O，且EF⊥CD，BE＝DF＝1.
1. （1）求EF的长；
2. （2）直接写出▱ABCD的面积.
答案解析收藏纠错 + 选题
20. (2020·和平模拟) 某校组织了一次比赛，甲、乙两队各有5人参加比赛，两队每人的比赛成绩（单位：分）如下：
甲队：7，8，9，6，10

乙队：10，9，5，8，8
1. （1）甲队成绩的中位数是分，乙队成绩的众数是分；
2. （2）计算乙队的平均成绩和方差；
3. （3）已知甲队成绩的方差为S²_甲＝2，则成绩波动较大的是队.
答案解析收藏纠错 + 选题
21. (2020·和平模拟) 如图，AB是⊙O的弦，直线BC与⊙O相切于点B，AD⊥BC，垂足为D，连接OA，OB.
1. （1）求证：AB平分∠OAD；
2. （2）当∠AOB＝100°，⊙O的半径为6cm时.
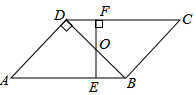
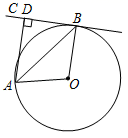
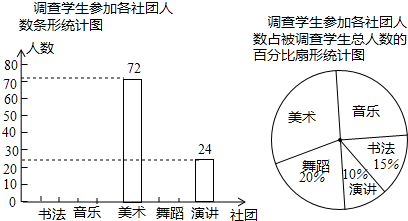
  ①直接写出扇形AOB的面积约为cm²（结果精确到1cm²）；
  
  ②点E是⊙O上一动点（点E不与点A、点B重合），连接AE，BE，请直接写出∠AEB＝°.
答案解析收藏纠错 + 选题
22. (2020·和平模拟) 某商店购进一批成本为每件40元的商品，若商店按单价不低于成本价，且不高于70元销售，且销售单价为正整数，经调查发现，该商品每天的销售量y(件)与销售单价x(元)之间的关系如表：

销售单价x/元

40

50

60

70

每天的销售量y/件

140

120

100

80
1. （1）请你认真分析表中所给的数据，用你学过的一次函数、反比例函数和二次函数中的一种来表示y与x之间的变化规律，说明选择这种函数的理由，并求出它的函数表达式和自变量的取值范圈.
2. （2）销售单价定为多少元时，才能使销售该商品每天获得的利润最大？最大利润是多少元？
答案解析收藏纠错 + 选题
23. (2020·和平模拟) 如图，在平面立角坐标系中，反比例函数y＝ $\text{[math]}$ （k≠0，x＜0）与一次函数y＝ax+b的图象交于点A(﹣3，1)、B(m，3).点C的坐标为(1，0)，连接AC，BC.
1. （1）求反比例函数和一次函数的表达式；
2. （2）当x＜0时，直接写出不等式 $\text{[math]}$ ≥ax+b的解集；
3. （3）若点M为y轴的正半轴上的动点，当△ACM是直角三角形时，直接写出点M的坐标.
答案解析收藏纠错 + 选题
24. (2020·和平模拟) 如图
1. （1）问题探究：如图1所示，有公共顶点A的两个正方形ABCD和正方形AEFG.AE＜AB，连接BE与DG，请判断线段BE与线段DG之间有怎样的数量关系和位置关系.并请说明理由.
2. （2）理解应用：如图2所示，有公共顶点A的两个正方形ABCD和正方形AEFG，AE＜AB，AB＝10，将正方形AEFG绕点A在平面内任意旋转，当∠ABE＝15°，且点D、E、G三点在同一条直线上时，请直接写出AE的长；
3. （3）拓展应用：如图3所示，有公共顶点A的两个矩形ABCD和矩形AEFG，AD＝4 $\text{[math]}$ ，AB＝4 $\text{[math]}$ ，AG＝4，AE＝4 $\text{[math]}$ ，将矩形AEFG绕点A在平面内任意旋转，连接BD，DE，点M，N分别是BD，DE的中点，连接MN，当点D、E、G三点在同一条直线上时，请直接写出MN的长
答案解析收藏纠错 + 选题
25. (2020·和平模拟) 如图，在平面直角坐标系中，矩形AOBC的边AO在x轴的负半轴上，边OB在y轴的负半轴上.且AO＝12，OB＝9.抛物线y＝﹣x²+bx+c经过点A和点B.
1. （1）求抛物线的表达式；
2. （2）在第二象限的抛物线上找一点M，连接AM，BM，AB，当△ABM面积最大时，求点M的坐标；
3. （3）点D是线段AO上的动点，点E是线段BO上的动点，点F是射线AC上的动点，连接EF，DF，DE，BD，且EF是线段BD的垂直平分线.当CF＝1时.
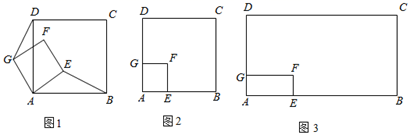
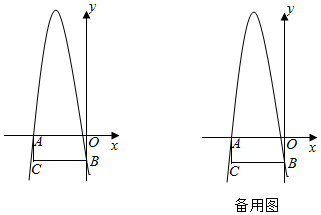
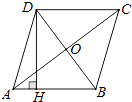
  ①直接写出点D的坐标；
  
  ②若△DEF的面积为30，当抛物线y＝﹣x²+bx+c经过平移同时过点D和点E时，请直接写出此时的抛物线的表达式.
答案解析收藏纠错 + 选题