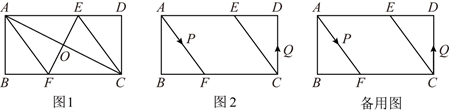一、选择题(本大题10小题,每小题3分,共30分)在每小题列出的四个选项中,只有一个是正确的。
-
-
-
A . 2,3,4
B . 5,12,13
C . 4,6,9
D . 5,11,13
-
-
A . 2
B . 3
C . 3.2
D . 4
-
A . 两对角线相等的四边形是矩形
B . 两对角线互相垂直的四边形是菱形
C . 两对角线互相垂直平分且相等的四边形是正方形
D . 一组对边相等另一组对边平行的四边形是平行四边形
-
A . 60°
B . 70°
C . 80°
D . 90°
-
A . 5
B . 6
C . 6.5
D . 12
-
-
10.
(2020八下·惠州期末)
甲、乙两人分别从
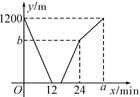
A,B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min , 又各自按原速前往目的地,甲、乙两人之间的距离

与甲所用时间

之间的函数关系如图所示.有下列说法:

,
B之间的距离为1200m;

乙行走的速度是甲的

倍;

;

以上结论正确的有


二、填空题(本大题7小题,每小题4分,共28分)
-
-
-
13.
(2020八下·惠州期末)
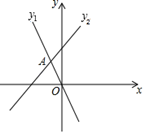
如图,函数
y1=﹣2
x和
y2=
ax+3的图象相交于点
A(﹣1,
m),则关于
x的不等式﹣2
x≥
ax+的解集是
.
-
-
-
-
17.
(2020八下·惠州期末)
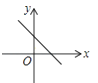
如图四边形
ABCD ,
AD∥
BC ,
AB⊥
BC ,
AD=1,
AB=2,
BC=3,
P为
AB边上的一动点,以
PD ,
PC为边作平行四边形
PCQD , 则对角线
PQ的长的最小值是
.

三、解答题(一)(本大题3小题,每小题6分,共18分)
-
-
19.
(2024八下·乌鲁木齐期中)
如图,在▱ABCD中,已知点E和点F分别在AD和BC上,且DE=BF,连结CE和AF,试说明四边形AFCE是平行四边形.
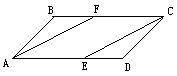
-
四、解答题(二)(本大题3小题,每小题8分,共24分)
-
21.
(2021八下·龙湖期末)
在开展“学雷锋社会实践”活动中,某校为了解全校1000名学生参加活动的情况,随机调查了50名学生每人参加活动的次数,并根据数据绘成如图的条形统计图:
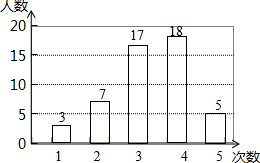
-
-
-
(3)
根据样本数据,估算该校1000名学生大约有多少人参加了4次实践活动.
-
22.
(2020八下·惠州期末)
如图,在菱形
ABCD中,对角线
AC与
BD交于点
O , 过点
C作
AC的垂线,过点
D作
BD的垂线,两直线相交于点
E .
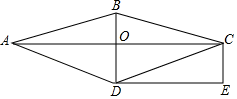
-
-
(2)
若
CE=1,

,求四边形的
ABCD面积.
-
23.
(2021八下·龙湖期末)
某工厂计划生产
A、
B两种产品共50件,已知
A产品成本2000元/件,售价2300元/件;
B种产品成本3000元/件,售价3500元/件,设该厂每天生产
A种产品
x件,两种产品全部售出后共可获利
y元.
-
-
(2)
如果该厂每天最多投入成本140000元,那么该厂生产的两种产品全部售出后最多能获利多少元?
五、解答题(三)(本大题2小题,每小题10分,共20分)
-
24.
(2020八下·惠州期末)
如图,直线
y=
kx+6与
x轴、
y轴分别相交于点
E、
F , 点
E的坐标为(﹣8,0),点
A的坐标为(﹣6,0),点
P是直线
EF上的一个动点.
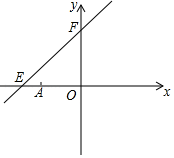
-
-
(2)
点P在第二象限内的直线EF上的运动过程中,写出△OPA的面积S与x的函整表达式,并写出自变量x的取值范围;
-
(3)
探究,当点P在直线EF上运动到时,△OPA的面积可能是15吗?若能,请求出点P的坐标;若不能,说明理由.
-
25.
(2020八下·惠州期末)
已知,矩形
ABCD中,AB=4cm,BC=8cm,
AC的垂直平分线
EF分别交
AD、
BC于点
E、
F , 垂足为
O .
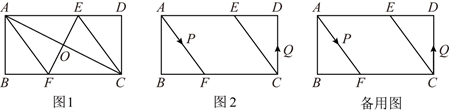
-
(1)
如图1,连接AF、CE,求证:四边形AFCE为菱形;
-
-
(3)
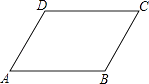
如图2,动点P、Q分别从A、C两点同时出发,沿ΔAFB和ΔCDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.若点Q的速度为每秒0.8cm,当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.
 B .
B . 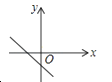 C .
C . 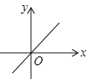 D .
D .