一、选择题:本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
-
-
A . 菱形的对角线互相垂直
B . 平行四边形的两组对边相等
C . 如果一个四边形是正方形,那么它的四条边相等
D . 如果一个四边形是矩形,那么它的对角线相等
-
A . 4,6,8
B . 6,8,9
C . 7,24,25
D . 5,11,12
-
-
A . 6
B . 18
C . 12
D . 24
-
7.
(2020八下·阳西期末)
如表是某校合唱团成员的年龄分布统计,则这组数据(年龄)的中位数是( )
| 年龄 | 13 | 14 | 15 | 16 |
| 频数 | 5 | 4 | 13 | 3 |
A . 15
B . 14
C . 13
D . 16
-
-
-
10.
(2020八下·阳西期末)
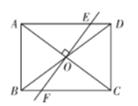
如图,在矩形ABCD中,

,

,过对角线交点

作

交AD于点E,交BC于点F,则DE的长是( )
A . 1
B .  C . 2
D .
C . 2
D . 
二、填空题(本大题共7个小题,每小题4分,共28分)
-
-
-
13.
(2020八下·阳西期末)
某校拟招聘一批优秀教师,其中某位教师笔试,试讲,面试三轮测试得分为92分,85分,90分.
若综合成绩笔试占40%,试讲占40%,面试占20%,则该名教师的综合成绩为分.
-
14.
(2020八下·阳西期末)
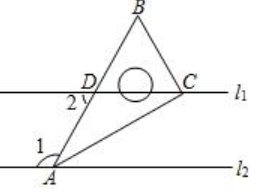
如图,已知直线

,含

角的三角板的直角顶点C在

上,

角的顶点A在

上,如果边AB与

的交点D是AB的中点,那么

-
-
16.
(2020八下·阳西期末)
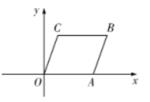
将平行四边形OABC放置在如图所示的平面直角坐标系中,点

为坐标原点,若点A的坐标为

,点C的坐标为

,则点B的坐标为
.
-
17.
(2020八下·阳西期末)
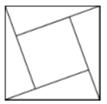
“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长的直角边长为

,较短的直角边长为

,若

,小正方形的面积为9,则大正方形的边长为
.
三、解答题:本大题共3个小题,每小题6分,共18分.
-
-
-
20.
(2020八下·阳西期末)
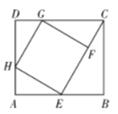
如图,在矩形ABCD中,

,

,菱形

的三个顶点

分别在矩形

的边

上,

,

,求证:四边形

为正方形.
四、解答题(二)(本大题3小题,每小题8分,共24分)
-
-
(1)
观察上面的解答过程,请写出

;
-
(2)
利用上面的解法,请化简:

.
-
22.
(2020八下·阳西期末)
某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如图所示的两幅不完整的统计图.
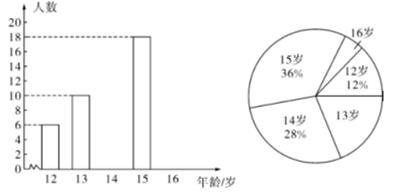
依据以上信息解答以下问题:
-
-
-
(3)
若该校一共有1800名学生,请估计该校年龄在15岁及以上的学生人数.
-
-
(1)
求证:

;
-
五、解答题(三)(本大题2小题,每小题10分,共20分)
-
24.
(2020八下·阳西期末)
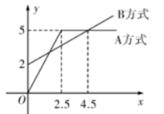
“

学习网”上网学习有

两种付费方式,上网学习时间

(时)与学习费用

(元)之间的函数关系如图所示.
-
(1)
当

时,分别求出

两种付费方式中

与

的函数解析式;
-
-
(3)
当学习时间为多少时,A方式的学习费用比B方式的学习费用高得最多?最多高多少?
-
25.
(2020八下·阳西期末)
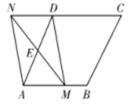
如图,在菱形ABCD中,

,

,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
-
-
-
(3)
若

,求证:四边形AMDN是菱形.
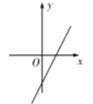 B .
B . 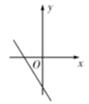 C .
C . 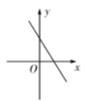 D .
D .