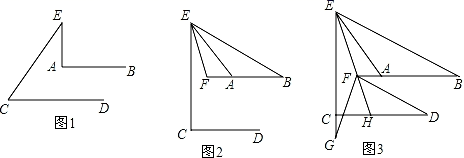
B .
B .  C .
C .  D .
D . 
①同位角相等;②等角的补角相等;③两直线平行,同旁内角相等;④在同一平面内,过一点有且只有一条直线与已知直线垂直.
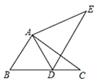


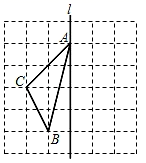
⑴在图中画出 关于直线l成轴对称的
;
⑵求 的面积;
⑶在直线l上找一点P,使PB+PC的长最短,标出点P(保留作图痕迹).

|
所挂物体的质量/千克 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
弹簧的长度/cm |
12 |
12.5 |
13 |
13.5 |
14 |
14.5 |
15 |
15.5 |
16 |