
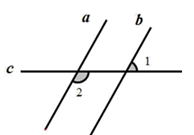
① ∠ 1+ ∠ 2= ∠ 5;② ∠ 1+ ∠ 3= ∠ 4;
③ ∠ 1+ ∠ 2+ ∠ 3= ∠ 6;④ ∠ 3+ ∠ 4= ∠ 2+ ∠ 5.
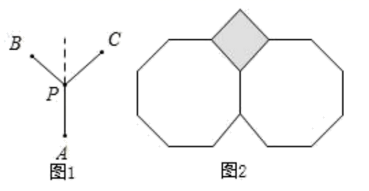
例如:若∠BPC=90°,则∠APB=∠APC=135°,图2就是一个符合要求的图形.
在所有符合要求的图形中,∠BPC的度数是.(∠BPC=90°除外)
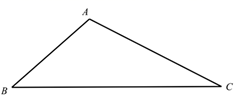
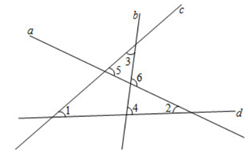
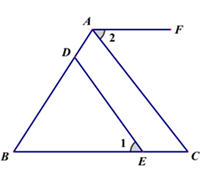
①面积一定相等的三角形是(不添加字母和辅助线);
②若∠BAC=120°,则∠AFC+∠FCE=°
|
甲从乙那里拿来10本 |
乙从甲那里拿来10本 |
|
|
甲拥有的图书 |
x+10 |
|
|
乙拥有的图书 |
|
y+10 |
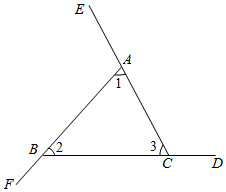
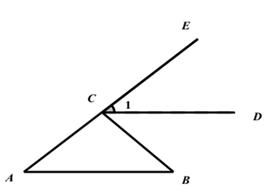
∠BAE、∠CBF、∠ACD是△ABC的三个外角.求证:∠BAE+∠CBF+∠ACD=360°
证法1:∵∠BAE、∠CBF、∠ACD是△ABC的三个外角
∴__▲_.
∴∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3)
∵_▲_.
∴∠BAE+∠CBF+∠ACD=360°
请把证法1补充完整,并用不同的方法完成证法2
( 1 )方舱医院由四部分组成,分别是废弃物处理单元、病房单元、技术保障单元、医疗功能单元;
( 2 )整个方舱医院占地面积为80000平方米;
( 3 )废弃物处理单元面积为总占地面积的5%;
( 4 )病房单元占地面积是技术保障单元占地面积的4倍;
( 5 )病房单元与医疗功能单元面积的和不高于总占地面积的85%,求医疗功能单元的最大面积.
分析问题:由于点P是平面上的任意点,要考虑全面,需对点P的位置进行如下分类.
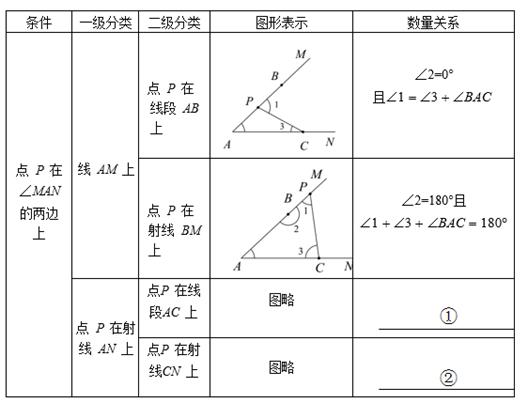
①;②。
若点P在区域①中,则所求数量关系为:▲ ;
若点P在区域②中,写出这4个角之间的数量关系,并利用图2加以证明.
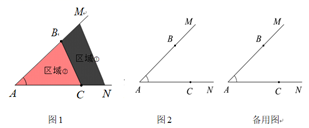
点P在∠MAN的外部时,直接写出当点P在该部分时这4个角之间的数量关系.