 C .
C .  D .
D . 
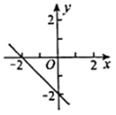 B .
B .  C .
C . 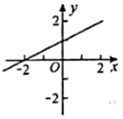 D .
D . 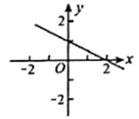
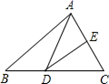
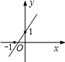
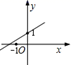 B .
B . 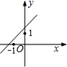 C .
C . 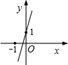 D .
D . 
|
C |
D |
总计/t |
|
|
A |
200 |
||
|
B |
x |
300 |
|
|
总计/t |
240 |
260 |
500 |