浙江省宁波市海曙区储能学校2020-2021学年八年级上学期...

更新时间：2024-07-13 浏览次数：205 类型：期中考试

一、选择题(本大题共10小题，每小题3分，共30分)

1. (2024八下·巴楚期中) 下列垃圾分类的图标（不含文字与字母部分）中，是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2020八上·柘城期中) 下列长度的三条线段不能组成三角形的是（）

A . 3，4，5 B . 1， $\text{[math]}$ ，2 C . 6，8，10 D . 1.5，2.5，4

答案解析收藏纠错 + 选题
3. (2020八上·海曙期中) 下列命题的逆命题是真命题的是（）

A . 对顶角相等 B . 等角对等边 C . 同角的余角相等 D . 全等三角形对应角相等

答案解析收藏纠错 + 选题
4. (2020八上·海曙期中) 下列不等式组的解集，在数轴上表示为如图所示的是（）

A . x>-1 B . -1<x≤2 C . -1≤x<2 D . x>-1或x≤2

答案解析收藏纠错 + 选题
5. (2020八上·海曙期中) 在平面直角坐标系中，与点P关于原点对称的点Q为(1，-3) ，则点P的坐标是（）

A . (1，3) B . (-1，-3) C . (1，-3) D . (-1，3)

答案解析收藏纠错 + 选题
6. (2020八上·海曙期中) △ABC中∠A，∠B，∠C的对边分别是a、b、c，下列命题为真命题的是（）

A . 如果∠A=2∠B=3∠C，则△ABC是直角三角形 B . 如果∠A：∠B：∠C=3：4：5，则△ABC是直角三角形 C . 如果a：b：c=1：2：2，则△ABC是直角三角形 D . 如果a：b：c=3：4： $\text{[math]}$ ，则△ABC是直角三角形

答案解析收藏纠错 + 选题
7. (2023八上·大连月考) 下列说法中：①线段是轴对称图形，②已知两腰就能确定等腰三角形的形状和大小，③等腰三角形的角平分线就是底边的垂直平分线，正确的有（）

A . 0个 B . 1个 C . 2个 D . 3个

答案解析收藏纠错 + 选题
8. (2020八上·海曙期中) 已知关于x的不等式组 $\text{[math]}$ 有解，则a的取值不可能是（）

A . 0 B . 1 C . 2 D . -2

答案解析收藏纠错 + 选题
9. (2020八上·海曙期中) 如图，把△ABC经过一定的变换得到△A'B'C' ，如果△ABC上点P的坐标为(x，y)，那么这个点在△A'B'C'中的对应点P'的坐标为（）

A . (-x，y-2) B . (-x，y+2) C . (-x+2，-y) D . (-x+2，y+2)

答案解析收藏纠错 + 选题
10. (2020八上·海曙期中) 如图，P是等边三角形ABC内一点，且PA=4，PB= $\text{[math]}$ ，PC=2，以下五个结论：①∠ BPC=120°；②∠APC=120°；③ $\text{[math]}$ ；④AB= $\text{[math]}$ ；⑤点P到△ABC三边的距离分别为PE，PF，PG，则有 $\text{[math]}$ 其中正确的有（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题

二、填空题(本大题共6小题，每小题3分，共18分)

11. (2020八上·海曙期中) 点(2，-3)在第象限

答案解析收藏纠错 + 选题
12. (2023八上·鄞州期末) “x的2倍与3的差是非负数．”用不等式表示为：．

答案解析收藏纠错 + 选题
13. (2020八上·海曙期中) 在直角三角形中，两条直角边的长分别是8和15，则斜边上的中线长是.

答案解析收藏纠错 + 选题
14. (2022八上·新昌期中) 如图，在△ABC中，AB=AC，DE是AB的中垂线，点D在AB上，点E在AC上，若△ABC的周长为25cm，△EBC的周长为18cm，则AC的长度为cm

答案解析收藏纠错 + 选题
15. (2020八上·海曙期中) 如图，在锐角△ABC中，AB= $\text{[math]}$ ，∠BAC= 45°，∠BAC的平分线交BC于点D， M，N分别是AD，AB上的动点，则BM+MN的最小值是

答案解析收藏纠错 + 选题
16. (2020八上·海曙期中) 如图所示“赵爽弦图”是由8个全等的直角三角形拼接而成的，记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S₁、S₂、S₃ ，若S₁+S₂+S₃=10，S₂的值是

答案解析收藏纠错 + 选题

三、解答题(本大题共8小题，共52分)

17. (2020八上·海曙期中) 解不等式3(2+x)>2x，并把解在数轴上表示出来

答案解析收藏纠错 + 选题
18. (2020八上·海曙期中) 在Rt△ABC中，∠ACB=90°，利用直尺和圆规作图

( 1 )作出△ABC的角平分线AE；

( 2 )若AC=5，BC=12，求出斜边AB上的高的长度

答案解析收藏纠错 + 选题
19. (2020八上·海曙期中) 如图，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ .

答案解析收藏纠错 + 选题
20. (2020八上·海曙期中) 如图，在直角坐标系中，长方形ABCD的三个顶点的坐标为A(1，1)，B(6，1)， D(1，4)，且AB∥x轴，点P(a，b-2)是长方形内一点(不含边界)
1. （1）求a，b的取值范围
2. （2）若将点P向左移动8个单位，再向上移动2个单位到点Q ，若点Q恰好与点C关于y轴对称，求a，b的值
答案解析收藏纠错 + 选题

21. (2020八上·海曙期中) 随着人们生活质量的提高，净水器已经慢慢走入了普通百姓家庭，某电器公司销售每台进价分别为2000元、1700元的 A、B两种型号的净水器，下表是近两周的销售情况：

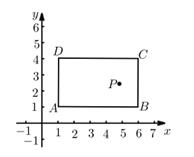
销售时段	销售数量		销售收入
销售时段	A种型号：	B种型号：	销售收入
第一周	3台	5台	18000元
第二周	4台	10台	31000元

（1）求A， B两种型号的净水器的销售单价．
（2）若电器公司准备用不多于54000元的金额采购这两种型号的净水器共30台，求A种型号的净水器最多能采购多少台？

答案解析收藏纠错 + 选题

22. (2020八上·海曙期中) 已知，DA，DB，DC是从点D出发的三条线段，且DA=DB=DC。
1. （1）如图①，若点D在线段AB上，连接AC，BC，试判断△ABC的形状，并说明理由。
2. （2）如图②，连接AC，BC，AB，且AB与CD相交于点E，若AC=BC，AB=16，DC=10，求CE和AC的长。
答案解析收藏纠错 + 选题
23. (2020八上·海曙期中) 如图，已知等边△ABC的边长为8，点P是AB边上的一个动点(与点A、B不重合)。直线是经过点P的一条直线，把△ABC沿直线折叠，点B的对应点是点B'
1. （1）如图1，当PB=4时，若点B'恰好在AC边上，则AB'的长度为
2. （2）如图2，当PB=5时，若直线l∥AC，则BB'的长度为
3. （3）如图3，点P在AB边上运动过程中，若直线始终垂直于AC，△ACB'的面积是否变化？若变化，说明理由；若不变化，求出面积
答案解析收藏纠错 + 选题
24. (2020八上·海曙期中) 定义：两边的平方和与这两边乘积的差等于第三边平方的三角形叫做“和谐三角形”。如图1在△ABC中，若AB²+AC²-AB·AC=BC² ，则△ABC是“和谐三角形”。
1. （1）等边三角形一定是“和谐三角形”，是命题(填“真”或“假”)。
2. （2）若Rt△ABC中，∠C=90°，AB=c，AC=b，BC=a，且b>a，若△ABC是“和谐三角形”，求a：b：c。
3. （3）如图2，在等边三角形ABC的边AC、BC上各取一点D、E，且AD<CD，AE、BD相交于点F，BG是△BEF的高，若△BGF是"和谐三角形”，且BG> FG。
  
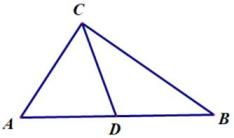
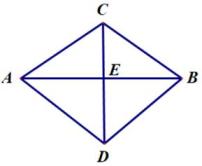
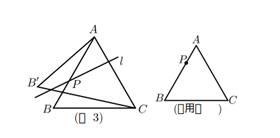
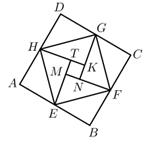
  ①求证：AD=CE
  
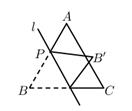
  ②连接CG，若∠GCB= CABD，那么线段AG、FE、CD能否组成一个“和谐三角形” ？若能，请给出证明；若不能，请说明理由。
答案解析收藏纠错 + 选题