2017年四川省乐山市中考数学试卷

更新时间：2024-07-12 浏览次数：1538 类型：中考真卷

一、选择题：

1. (2017·乐山) ﹣2的倒数是（）

A . ﹣ $\text{[math]}$ B . $\text{[math]}$ C . 2 D . ﹣2

答案解析收藏纠错 + 选题
2. (2017·乐山) 随着经济发展，人民的生活水平不断提高，旅游业快速增长，2016年国民出境旅游超过120 000 000人次，将120 000 000用科学记数法表示为（）

A . 1.2×10⁹ B . 12×10⁷ C . 0.12×10⁹ D . 1.2×10⁸

答案解析收藏纠错 + 选题
3. (2017·乐山) 下列图形中，既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2021·原州模拟) 含30°角的直角三角板与直线l₁、l₂的位置关系如图所示，已知l₁∥l₂ ， ∠ACD=∠A，则∠1=（）

A . 70° B . 60° C . 40° D . 30°

答案解析收藏纠错 + 选题
5. (2017·乐山) 下列说法正确的是（）

A . 打开电视，它正在播广告是必然事件 B . 要考察一个班级中的学生对建立生物角的看法适合用抽样调查 C . 在抽样调查过程中，样本容量越大，对总体的估计就越准确 D . 甲、乙两人射中环数的方差分别为S_甲²=2，S_乙²=4，说明乙的射击成绩比甲稳定

答案解析收藏纠错 + 选题
6. (2017·乐山) 若a²﹣ab=0（b≠0），则 $\text{[math]}$ =（）

A . 0 B . $\text{[math]}$ C . 0或 $\text{[math]}$ D . 1或 2

答案解析收藏纠错 + 选题
7. (2017·乐山) 如图是“明清影视城”的一扇圆弧形门，小红到影视城游玩，他了解到这扇门的相关数据：这扇圆弧形门所在的圆与水平地面是相切的，AB=CD=0.25米，BD=1.5米，且AB，CD与水平地面都是垂直的．根据以上数据，请你帮小红计算出这扇圆弧形门的最高点离地面的距离是（）

A . 2米 B . 2.5米 C . 2.4米 D . 2.1米

答案解析收藏纠错 + 选题
8. (2017·乐山) 已知x+ $\text{[math]}$ =3，则下列三个等式：①x²+ $\text{[math]}$ =7，②x﹣ $\text{[math]}$ ，③2x²﹣6x=﹣2中，正确的个数有（）

A . 0个 B . 1个 C . 2个 D . 3个

答案解析收藏纠错 + 选题
9. (2024·清城模拟) 已知二次函数y=x²﹣2mx（m为常数），当﹣1≤x≤2时，函数值y的最小值为﹣2，则m的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2017·乐山) 如图，平面直角坐标系xOy中，矩形OABC的边OA、OC分别落在x、y轴上，点B坐标为（6，4），反比例函数y= $\text{[math]}$ 的图象与AB边交于点D，与BC边交于点E，连结DE，将△BDE沿DE翻折至△B'DE处，点B'恰好落在正比例函数y=kx图象上，则k的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题：

11. (2017·乐山) 3^﹣²=．

答案解析收藏纠错 + 选题
12. (2023九下·庆元模拟) 二元一次方程组 $\text{[math]}$ = $\text{[math]}$ =x+2的解是．

答案解析收藏纠错 + 选题
13. (2022·温州模拟) 如图，直线a、b垂直相交于点O，曲线C关于点O成中心对称，点A的对称点是点A'，AB⊥a于点B，A'D⊥b于点D．若OB=3，OD=2，则阴影部分的面积之和为．

答案解析收藏纠错 + 选题
14. (2017·乐山) 点A，B，C在格点图中的位置如图5所示，格点小正方形的边长为1，则点C到线段AB所在直线的距离是．

答案解析收藏纠错 + 选题
15. (2017·乐山) 庄子说：“一尺之椎，日取其半，万世不竭”．这句话（文字语言）表达了古人将事物无限分割的思想，用图形语言表示为图1，按此图分割的方法，可得到一个等式（符号语言）：1= $\text{[math]}$ + $\text{[math]}$ + $\text{[math]}$ +…+ $\text{[math]}$ +…．
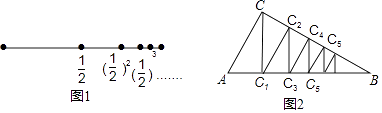
图2也是一种无限分割：在△ABC中，∠C=90°，∠B=30°，过点C作CC₁⊥AB于点C₁ ，再过点C₁作C₁C₂⊥BC于点C₂ ，又过点C₂作C₂C₃⊥AB于点C₃ ，如此无限继续下去，则可将利△ABC分割成△ACC₁、△CC₁C₂、△C₁C₂C₃、△C₂C₃C₄、…、△C_n_﹣₂C_n_﹣₁C_n、…．假设AC=2，这些三角形的面积和可以得到一个等式是．

答案解析收藏纠错 + 选题
16. (2017·乐山) 对于函数y=xⁿ+x^m ，我们定义y'=nxⁿ^﹣¹+mx^m^﹣¹（m、n为常数）．
例如y=x⁴+x² ，则y'=4x³+2x．
已知：y= $\text{[math]}$ x³+（m﹣1）x²+m²x．
1. （1）若方程y′=0有两个相等实数根，则m的值为；
2. （2）若方程y′=m﹣ $\text{[math]}$ 有两个正数根，则m的取值范围为．
答案解析收藏纠错 + 选题

三、综合题

17. (2017·乐山) 计算：2sin60°+|1﹣ $\text{[math]}$ |+2017⁰﹣ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2017·乐山) 求不等式组 $\text{[math]}$ 的所有整数解．

答案解析收藏纠错 + 选题
19. (2017·乐山) 如图，延长▱ABCD的边AD到F，使DF=DC，延长CB到点E，使BE=BA，分别连结点A，E和C，F．求证：AE=CF．

答案解析收藏纠错 + 选题
20. (2017·乐山) 化简：（ $\text{[math]}$ ﹣ $\text{[math]}$ ）÷ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
21. (2017·乐山) 为了了解我市中学生参加“科普知识”竞赛成绩的情况，随机抽查了部分参赛学生的成绩，整理并制作出如下的统计表和统计图，如图所示．请根据图表信息解答下列问题：
组别
分数段（分）
频数
频率
A组
60≤x＜70
30
0.1
B组
70≤x＜80
90
n
C组
80≤x＜90
m
0.4
D组
90≤x＜100
60
0.2
1. （1）在表中：m=，n=；
2. （2）补全频数分布直方图；
3. （3）小明的成绩是所有被抽查学生成绩的中位数，据此推断他的成绩在组；
4. （4） 4个小组每组推荐1人，然后从4人中随机抽取2人参加颁奖典礼，恰好抽中A、C两组学生的概率是多少？并列表或画树状图说明．
答案解析收藏纠错 + 选题
22. (2017·乐山) 如图，在水平地面上有一幢房屋BC与一棵树DE，在地面观测点A处测得屋顶C与树梢D的仰角分别是45°与60°，∠CAD=60°，在屋顶C处测得∠DCA=90°．若房屋的高BC=6米，求树高DE的长度．

答案解析收藏纠错 + 选题
23. (2017·乐山) 某公司从2014年开始投入技术改进资金，经技术改进后，其产品的成本不断降低，具体数据如下表：
年度
2013
2014
2015
2016
投入技改资金x（万元）
2.5
3
4
4.5
产品成本y（万元/件）
7.2
6
4.5
4
1. （1）请你认真分析表中数据，从一次函数和反比例函数中确定哪一个函数能表示其变化规律，给出理由，并求出其解析式；
2. （2）按照这种变化规律，若2017年已投入资金5万元．
  ①预计生产成本每件比2016年降低多少万元？
  ②若打算在2017年把每件产品成本降低到3.2万元，则还需要投入技改资金多少万元？（结果精确到0.01万元）．
答案解析收藏纠错 + 选题
24. (2021·新吴模拟) 如图，以AB边为直径的⊙O经过点P，C是⊙O上一点，连结PC交AB于点E，且∠ACP=60°，PA=PD．
1. （1）试判断PD与⊙O的位置关系，并说明理由；
2. （2）若点C是弧AB的中点，已知AB=4，求CE•CP的值．
答案解析收藏纠错 + 选题
25. (2022·温州模拟) 在四边形ABCD中，∠B+∠D=180°，对角线AC平分∠BAD．
1. （1）如图1，若∠DAB=120°，且∠B=90°，试探究边AD、AB与对角线AC的数量关系并说明理由．
2. （2）如图2，若将（1）中的条件“∠B=90°”去掉，（1）中的结论是否成立？请说明理由．
3. （3）如图3，若∠DAB=90°，探究边AD、AB与对角线AC的数量关系并说明理由．
答案解析收藏纠错 + 选题
26. (2017·乐山) 如图1，抛物线C₁：y=x²+ax与C₂：y=﹣x²+bx相交于点O、C，C₁与C₂分别交x轴于点B，A，且B为线段AO的中点．
1. （1）求 $\text{[math]}$ 的值；
2. （2）若OC⊥AC，求△OAC的面积；
3. （3）抛物线C₂的对称轴为l，顶点为M，在（2）的条件下：
  ①点P为抛物线C₂对称轴l上一动点，当△PAC的周长最小时，求点P的坐标；
  ②如图2，点E在抛物线C₂上点O与点M之间运动，四边形OBCE的面积是否存在最大值？若存在，求出面积的最大值和点E的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题