2016年浙江省台州市中考数学试卷

更新时间：2024-07-12 浏览次数：1161 类型：中考真卷

一、选择题

1. (2016·台州) 下列各数中，比﹣2小的数是（　　）

A . ﹣3 B . ﹣1 C . 0 D . 2

答案解析收藏纠错 + 选题
2. (2022·平遥模拟)
如图所示几何体的俯视图是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2016·台州) 我市今年一季度国内生产总值为77643000000元，这个数用科学记数法表示为（　　）

A . 0.77643×10¹¹ B . 7.7643×10¹¹ C . 7.7643×10¹⁰ D . 77643×10⁶

答案解析收藏纠错 + 选题
4. (2023九下·成都模拟) 下列计算正确的是（　　）

A . x²+x²=x⁴ B . 2x³﹣x³=x³ C . x²•x³=x⁶ D . （x²）³=x⁵

答案解析收藏纠错 + 选题
5. (2016·台州) 质地均匀的骰子六个面分别刻有1到6的点数，掷两次骰子，得到向上一面的两个点数，则下列事件中，发生可能性最大的是（　　）

A . 点数都是偶数 B . 点数的和为奇数 C . 点数的和小于13 D . 点数的和小于2

答案解析收藏纠错 + 选题
6. (2016·台州) 化简 $\text{[math]}$ 的结果是（　　）

A . ﹣1 B . 1 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2016·台州)
如图，数轴上点A，B分别对应1，2，过点B作PQ⊥AB，以点B为圆心，AB长为半径画弧，交PQ于点C，以原点O为圆心，OC长为半径画弧，交数轴于点M，则点M对应的数是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2016·台州) 有x支球队参加篮球比赛，共比赛了45场，每两队之间都比赛一场，则下列方程中符合题意的是（　　）

A . $\text{[math]}$ x（x﹣1）=45 B . $\text{[math]}$ x（x+1）=45 C . x（x﹣1）=45 D . x（x+1）=45

答案解析收藏纠错 + 选题
9. 小红用次数最少的对折方法验证了一条四边形丝巾的形状是正方形，她对折了（　　）

A . 1次 B . 2次 C . 3次 D . 4次

答案解析收藏纠错 + 选题
10. (2016·台州)
如图，在△ABC中，AB=10，AC=8，BC=6，以边AB的中点O为圆心，作半圆与AC相切，点P，Q分别是边BC和半圆上的动点，连接PQ，则PQ长的最大值与最小值的和是（　　）

A . 6 B . 2 $\text{[math]}$ +1 C . 9 D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2016·台州) 因式分解：x²﹣6x+9=．

答案解析收藏纠错 + 选题
12. (2016·台州)
如图，把三角板的斜边紧靠直尺平移，一个顶点从刻度“5”平移到刻度“10”，则顶点C平移的距离CC′= ．

答案解析收藏纠错 + 选题
13. (2016·台州)
如图，△ABC的外接圆O的半径为2，∠C=40°，则 $\text{[math]}$ 的长是．

答案解析收藏纠错 + 选题
14. (2016·台州) 不透明袋子中有1个红球、2个黄球，这些球除颜色外无其他差别，从袋子中随机摸出1个球后放回，再随机摸出1个球，两次摸出的球都是黄球的概率是．

答案解析收藏纠错 + 选题
15. (2016·台州)
如图，把一个菱形绕着它的对角线的交点旋转90°，旋转前后的两个菱形构成一个“星形”（阴影部分），若菱形的一个内角为60°，边长为2，则该“星形”的面积是．

答案解析收藏纠错 + 选题
16. (2024九上·楚雄月考) 竖直上抛的小球离地高度是它运动时间的二次函数，小军相隔1秒依次竖直向上抛出两个小球，假设两个小球离手时离地高度相同，在各自抛出后1.1秒时到达相同的最大离地高度，第一个小球抛出后t秒时在空中与第二个小球的离地高度相同，则t=．

答案解析收藏纠错 + 选题

三、解答题

17. (2016·台州) 计算： $\text{[math]}$ ﹣|﹣ $\text{[math]}$ |+2^﹣¹ ．

答案解析收藏纠错 + 选题
18. (2016·台州) 解方程： $\text{[math]}$ ﹣ $\text{[math]}$ =2．

答案解析收藏纠错 + 选题
19. (2016·台州)
如图，点P在矩形ABCD的对角线AC上，且不与点A，C重合，过点P分别作边AB，AD的平行线，交两组对边于点E，F和G，H．
1. （1）求证：△PHC≌△CFP；
2. （2）证明四边形PEDH和四边形PFBG都是矩形，并直接写出它们面积之间的关系．
答案解析收藏纠错 + 选题
20. (2016·台州)
保护视力要求人写字时眼睛和笔端的距离应超过30cm，图1是一位同学的坐姿，把他的眼睛B，肘关节C和笔端A的位置关系抽象成图2的△ABC，已知BC=30cm，AC=22cm，∠ACB=53°，他的这种坐姿符合保护视力的要求吗？请说明理由．（参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈1.3）

答案解析收藏纠错 + 选题
21. (2021七下·贺兰期中)
请用学过的方法研究一类新函数y= $\text{[math]}$ （k为常数，k≠0）的图象和性质．
1. （1）在给出的平面直角坐标系中画出函数y= $\text{[math]}$ 的图象；
2. （2）对于函数y= $\text{[math]}$ ，当自变量x的值增大时，函数值y怎样变化？
答案解析收藏纠错 + 选题
22. (2016·台州)
为了保护视力，学校开展了全校性的视力保健活动，活动前，随机抽取部分学生，检查他们的视力，结果如图所示（数据包括左端点不包括右端点，精确到0.1）；活动后，再次检查这部分学生的视力，结果如表所示．
分组
频数
4.0≤x＜4.2
2
4.2≤x＜4.4
3
4.4≤x＜4.6
5
4.6≤x＜4.8
8
4.8≤x＜5.0
17
5.0≤x＜5.2
5
1. （1）求所抽取的学生人数；
2. （2）若视力达到4.8及以上为达标，估计活动前该校学生的视力达标率；
3. （3）请选择适当的统计量，从两个不同的角度分析活动前后相关数据，并评价视力保健活动的效果．
答案解析收藏纠错 + 选题
23. (2016·台州)
定义：有三个内角相等的四边形叫三等角四边形．
1. （1）三等角四边形ABCD中，∠A=∠B=∠C，求∠A的取值范围；
2. （2）如图，折叠平行四边形纸片DEBF，使顶点E，F分别落在边BE，BF上的点A，C处，折痕分别为DG，DH．求证：四边形ABCD是三等角四边形．
3. （3）三等角四边形ABCD中，∠A=∠B=∠C，若CB=CD=4，则当AD的长为何值时，AB的长最大，其最大值是多少？并求此时对角线AC的长．
答案解析收藏纠错 + 选题
24. (2016·台州)
【操作发现】在计算器上输入一个正数，不断地按“ ”键求算术平方根，运算结果越来越接近1或都等于1．
【提出问题】输入一个实数，不断地进行“乘以常数k，再加上常数b”的运算，有什么规律？
【分析问题】我们可用框图表示这种运算过程（如图a）．
也可用图象描述：如图1，在x轴上表示出x₁ ，先在直线y=kx+b上确定点（x₁ ， y₁），再在直线y=x上确定纵坐标为y₁的点（x₂ ， y₁），然后再x轴上确定对应的数x₂ ， …，以此类推．
【解决问题】研究输入实数x₁时，随着运算次数n的不断增加，运算结果x，怎样变化．
1. （1）若k=2，b=﹣4，得到什么结论？可以输入特殊的数如3，4，5进行观察研究；
2. （2）若k＞1，又得到什么结论？请说明理由；
3. （3） ①若k=﹣ $\text{[math]}$ ，b=2，已在x轴上表示出x₁（如图2所示），请在x轴上表示x₂ ， x₃ ， x₄ ，并写出研究结论；
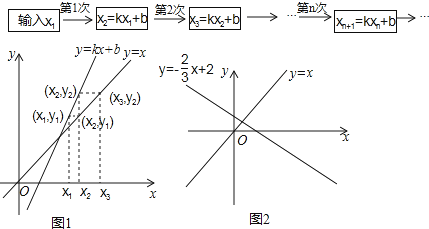
  ②若输入实数x₁时，运算结果x_n互不相等，且越来越接近常数m，直接写出k的取值范围及m的值（用含k，b的代数式表示）
答案解析收藏纠错 + 选题