陕西省榆林市2020-2021学年高三上学期理数第一次高考模...

更新时间：2021-02-23 浏览次数：190 类型：高考模拟

一、单选题

1. (2021·榆林模拟) 若复数z为纯虚数，且 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . -2 D . 2

答案解析收藏纠错 + 选题
2. (2021·榆林模拟) 集合 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021·榆林模拟) 如图，角 $\text{[math]}$ 的顶点与原点O重合，始边与x轴的非负半轴重合，终边与单位圆O分别交于A，B两点，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021·榆林模拟) 下列四个函数：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ，其中定义域与值域相同的函数的个数为（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
5. (2024高一下·江川月考) 在△ $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 边上的中线，E为 $\text{[math]}$ 的中点，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
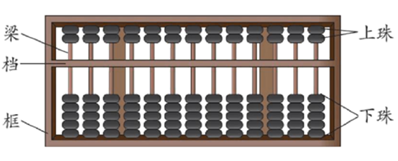
6. (2021·榆林模拟) 算盘是中国传统的计算工具，是中国人在长期使用算筹的基础上发明的，是中国古代一项伟大的、重要的发明，在阿拉伯数字出现前是全世界广为使用的计算工具.“珠算”一词最早见于东汉徐岳所撰的《数术记遗》，其中有云：“珠算控带四时，经纬三才.”北周甄鸾为此作注，大意是：把木板刻为3部分，上、下两部分是停游珠用的，中间一部分是作定位用的.下图是一把算盘的初始状态，自右向左，分别是个位、十位、百位、 $\text{[math]}$ ，上面一粒珠（简称上珠）代表5，下面一粒珠（简称下珠）是1，即五粒下珠的大小等于同组一粒上珠的大小.现在从个位和十位这两组中随机选择往下拨一粒上珠，往上拨2粒下珠，算盘表示的数为质数（除了1和本身没有其它的约数）的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021·榆林模拟) 已知 $\text{[math]}$ 是两条直线， $\text{[math]}$ 是两个平面，则 $\text{[math]}$ 的一个充分条件是（）

A . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021·榆林模拟) 若 $\text{[math]}$ ，则（）

A . 图像关于直线 $\text{[math]}$ 对称 B . 图像关于 $\text{[math]}$ 对称 C . 最小正周期为 $\text{[math]}$ D . 在 $\text{[math]}$ 上单调递增

答案解析收藏纠错 + 选题
9. (2021·榆林模拟) 在 $\text{[math]}$ 中，内角A，B，C所对边分别为a，b，c，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的面积为 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021·榆林模拟) 已知双曲线 $\text{[math]}$ 的左､右焦点分别为 $\text{[math]}$ ，过 $\text{[math]}$ 的直线与双曲线的左､右两支分别交于A，B两点，若 $\text{[math]}$ 为等边三角形，则双曲线的离心率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 3

答案解析收藏纠错 + 选题
11. (2021·榆林模拟) 设 $\text{[math]}$ ，随机变量的分布

$\text{[math]}$

-1

0

1

P

$\text{[math]}$

a

b

则当a在 $\text{[math]}$ 内增大时，（）

A . $\text{[math]}$ 增大， $\text{[math]}$ 增大 B . $\text{[math]}$ 增大， $\text{[math]}$ 减小 C . $\text{[math]}$ 减小， $\text{[math]}$ 增大 D . $\text{[math]}$ 减小， $\text{[math]}$ 减小

答案解析收藏纠错 + 选题
12. (2021高二下·成都月考) 已知定义在R上的偶函数 $\text{[math]}$ 满足 $\text{[math]}$ ，且 $\text{[math]}$ 在 $\text{[math]}$ 上递减.若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则a，b，c的大小关系为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. (2021·榆林模拟) 若二项式 $\text{[math]}$ 的展开式中二项式系数的和为64，则展开式中的常数项为.

答案解析收藏纠错 + 选题
14. (2021·榆林模拟) 过抛物线 $\text{[math]}$ 的焦点F的直线l与抛物线交于A，B两点，若 $\text{[math]}$ ，则 $\text{[math]}$ (O为坐标原点)的面积为.

答案解析收藏纠错 + 选题
15. (2021·榆林模拟) 已知一个棱长为1的正方体内接于半球体，即正方体的上底面的四个顶点在球面上，下底面的四个顶点在半球体的底面圆内，则该半球体(包括底面)的表面积为.

答案解析收藏纠错 + 选题
16. (2021·榆林模拟) 若 $\text{[math]}$ ，则下面不等式正确的是.
① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ；⑤ $\text{[math]}$ .

答案解析收藏纠错 + 选题

三、解答题

17. (2021·榆林模拟) 已知数列 $\text{[math]}$ 是等差数列， $\text{[math]}$ 是数列 $\text{[math]}$ 的前n项和， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）求数列 $\text{[math]}$ 的通项公式；
2. （2）数列 $\text{[math]}$ 满足 $\text{[math]}$ ，求数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和 $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2021·榆林模拟) 为了推进分级诊疗，实现“基层首诊､双向转诊､急慢分治､上下联动”的诊疗模式，某城市自2020年起全面推行家庭医生签约服务.已知该城市居民约为1000万，从0岁到100岁的居民年龄结构的频率分布直方图如图1所示.为了解各年龄段居民签约家庭医生的情况，现调查了1000名年满18周岁的居民，各年龄段被访者签约率如图2所示.
1. （1）估计该城市年龄在50岁以上且已签约家庭医生的居民人数；
2. （2）据统计，该城市被访者的签约率约为44%.为把该城市年满18周岁居民的签约率提高到55%以上，应着重提高图2中哪个年龄段的签约率？并根据已有数据陈述理由.
答案解析收藏纠错 + 选题
19. (2021·榆林模拟) 如图，在正四面体 $\text{[math]}$ 中，点E，F分别是 $\text{[math]}$ 的中点，点G，H分别在 $\text{[math]}$ 上，且 $\text{[math]}$ ， $\text{[math]}$ .
1. （1）求证：直线 $\text{[math]}$ 必相交于一点，且这个交点在直线 $\text{[math]}$ 上；
2. （2）求直线 $\text{[math]}$ 与平面 $\text{[math]}$ 所成角的正弦值.
答案解析收藏纠错 + 选题
20. (2021·榆林模拟) 已知椭圆 $\text{[math]}$ 与抛物线 $\text{[math]}$ 有相同的焦点 $\text{[math]}$ ，抛物线 $\text{[math]}$ 的准线交椭圆 $\text{[math]}$ 于 $\text{[math]}$ ， $\text{[math]}$ 两点，且 $\text{[math]}$ .
1. （1）求椭圆 $\text{[math]}$ 与抛物线 $\text{[math]}$ 的方程；
2. （2） $\text{[math]}$ 为坐标原点，若 $\text{[math]}$ 为椭圆 $\text{[math]}$ 上任意一点，以 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径的圆 $\text{[math]}$ 与椭圆 $\text{[math]}$ 的焦点 $\text{[math]}$ 为圆心，以 $\text{[math]}$ 为半径的圆 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点，求证： $\text{[math]}$ 为定值.
答案解析收藏纠错 + 选题
21. (2021·榆林模拟) 已知函数 $\text{[math]}$ .
1. （1）设 $\text{[math]}$ ，求 $\text{[math]}$ 的单调区间；
2. （2）求证：存在恰有2个切点的曲线 $\text{[math]}$ 的切线.
答案解析收藏纠错 + 选题
22. (2021·榆林模拟) 在直角坐标系 $\text{[math]}$ 中，直线l过点 $\text{[math]}$ ，倾斜角为 $\text{[math]}$ .以原点O为极点，x轴的非负半轴为极轴建立极坐标系，曲线C的极坐标方程为： $\text{[math]}$ .
1. （1）求直线l的参数方程与曲线C的直角坐标方程；
2. （2）若直线l交曲线C于A，B两点，M为 $\text{[math]}$ 中点，且满足 $\text{[math]}$ 成等比数列，求直线l的斜率.
答案解析收藏纠错 + 选题
23. (2021·榆林模拟) 已知函数 $\text{[math]}$ .
1. （1）当 $\text{[math]}$ 时，求 $\text{[math]}$ 的最小值；
2. （2）当 $\text{[math]}$ 时，不等式 $\text{[math]}$ 恒成立，求实数a的取值范围.
答案解析收藏纠错 + 选题