安徽省六安市2020-2021学年九年级上学期数学期末试卷

更新时间：2021-03-29 浏览次数：209 类型：期末考试

一、单选题

1. (2020九上·六安期末) 下列图形中，绕某个点旋转72度后能与自身重合的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2021九上·凤山期中) 若关于x的一元二次方程的两个根为x₁=1，x₂=2，则这个方程可能是（）

A . x²-3x+2=0 B . x²+3x+2=0 C . x²+3x-2=0 D . x²-2x+3=0

答案解析收藏纠错 + 选题
3. (2020九上·六安期末) 下列事件是必然事件的是( )

A . 某运动员射击一次击中靶心 B . 抛一枚硬币，正面朝上 C . 3个人分成两组，一定有2个人分在一组 D . 明天一定是晴天

答案解析收藏纠错 + 选题
4. (2023九上·香坊月考) 把抛物线y=﹣x²向左平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为（）

A . y=﹣（x﹣1）²﹣3 B . y=﹣（x+1）²﹣3 C . y=﹣（x﹣1）²+3 D . y=﹣（x+1）²+3

答案解析收藏纠错 + 选题
5. (2020九上·六安期末) 若 $\text{[math]}$ 是二次函数，且开口向上，则m的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 0

答案解析收藏纠错 + 选题
6. (2020九上·六安期末) 现有A、B两枚均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6）．用小莉掷A立方体朝上的数字为 $\text{[math]}$ 、小明掷B立方体朝上的数字为 $\text{[math]}$ 来确定点P（ $\text{[math]}$ ），那么他们各掷一次所确定的点P落在已知抛物线 $\text{[math]}$ 上的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020九上·六安期末) 已知一个圆锥的底面半径为3cm，母线长为10cm，则这个圆锥的侧面积为（　　）

A . 15πcm² B . 30πcm² C . 60πcm² D . 3 $\text{[math]}$ cm²

答案解析收藏纠错 + 选题
8. (2020九上·六安期末)
如图，在平面直角坐标系中，⊙P的圆心是（2，a）（a＞2），半径为2，函数y=x的图象被⊙P截得的弦AB的长为 $\text{[math]}$ ，则a的值是（）

A . 2 $\text{[math]}$ B . 2+ $\text{[math]}$ C . 2 $\text{[math]}$ D . 2+ $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020九上·六安期末) 如图，AB是⊙O的直径，弦CD⊥AB，∠CDB＝30°，CD＝2 $\text{[math]}$ ，则阴影部分图形的面积为（）

A . 4π B . 2π C . π D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2020九上·六安期末) 二次函数y=ax²+bx+c图象如图，下列正确的个数为（）
①bc＞0；

②2a﹣3c＜0；

③2a+b＞0；

④ax²+bx+c=0有两个解x₁ ， x₂ ， x₁＞0，x₂＜0；

⑤a+b+c＞0；

⑥当x＞1时，y随x增大而减小．

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题

二、填空题

11. (2020九上·六安期末) 已知关于x的二次方程（1﹣2k）x²﹣2x﹣1=0有实数根，则k的取值范围是．

答案解析收藏纠错 + 选题
12. (2020九上·六安期末) 如图，等边△ADE由△ABC绕点A逆时针旋转40°得到，其中AD与BC相交于点F，则∠AFB=．

答案解析收藏纠错 + 选题
13. (2020九上·六安期末) 如图，在Rt $\text{[math]}$ AOB中，OA=OB=3 ，⊙O的半径为1，点P是AB边上的动点，过点P作⊙O的一条切线PQ（点Q为切点），则切线PQ的最小值为．

答案解析收藏纠错 + 选题
14. (2021九上·恩施期末)
二次函数 $\text{[math]}$ 的图象如图，点O为坐标原点，点A在y轴的正半轴上，点B、C在二次函数 $\text{[math]}$ 的图象上，四边形OBAC为菱形，且∠OBA=120°，则菱形OBAC的面积为 .

答案解析收藏纠错 + 选题

三、解答题

15. (2021九上·茂名月考) 解方程
1. （1） x²–9 = 0
2. （2） x²+4x -1= 0
答案解析收藏纠错 + 选题
16. (2020九上·六安期末) 已知关于x的方程x²－（2k－1）x+k²=0有两个实数根x₁ ， x₂ ．
1. （1）求k的取值范围；
2. （2）若∣x₁+x₂∣= x₁x₂-1，求k的值．
答案解析收藏纠错 + 选题
17. (2020九上·六安期末) 已知二次函数y=﹣x²+x+4．
1. （1）求抛物线的顶点坐标和对称轴；
2. （2）当x取何值时，y随x的增大而增大？当x取何值时，y随x的增大而减小？当x取何值时，y有最大值还是最小值？是多少？
答案解析收藏纠错 + 选题
18. (2020九上·六安期末) 如图，在△ABC中，∠ACB=90°，E为BC上一点，以CE为直径作⊙O，AB与⊙O相切于点D，连接CD，若BE=OE=2．
1. （1）求证：∠A=2∠DCB；
2. （2）求图中阴影部分的面积（结果保留π和根号）．
答案解析收藏纠错 + 选题
19. (2020九上·六安期末) 如图所示，正方形网格中，△ABC为格点三角形（即三角形的顶点都在格点上）．

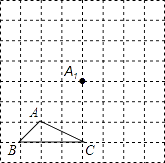
（1）把△ABC沿BA方向平移后，点A移到点A₁ ，在网格中画出平移后得到的△A₁B₁C₁；
（2）把△A₁B₁C₁绕点A₁按逆时针方向旋转90°，在网格中画出旋转后的△A₁B₂C₂；
（3）如果网格中小正方形的边长为1，求点B经过（1）、（2）变换的路径总长．

答案解析收藏纠错 + 选题
20. (2020九上·六安期末) 小明和小亮玩一个游戏：三张大小、质地都相同的卡片上分别标有数字3、4、5，现将标有数字的一面朝下．小明从中任意抽取一张，记下数字后放回洗匀，然后小亮从中任意抽取一张，计算小明和小亮抽得的两个数字之和．如果和为奇数，则小明胜；和为偶数，则小亮胜．
1. （1）请你用画树状图或列表的方法，求出这两数和为8的概率；
2. （2）你认为这个游戏对双方公平吗？说说你的理由．
答案解析收藏纠错 + 选题
21. (2020九上·六安期末) 列方程（组）解应用题：
据媒体报道，2011年某市市民到郊区旅游总人数约500万人，2013年到郊区旅游总

人数增长到约720万人．
1. （1）求这两年该市市民到郊区旅游总人数的年平均增长率．
2. （2）若该市到郊区旅游的总人数年平均增长率不变，请你预计2014年有多少市民到郊区旅游．
答案解析收藏纠错 + 选题
22. (2020九上·六安期末) 某市政府大力扶持大学生创业．李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数： $\text{[math]}$ ．
1. （1）设李明每月获得利润为w（元），当销售单价定为多少元时，每月可获得最大利润？
2. （2）如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？
3. （3）根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？
  （成本＝进价×销售量）
答案解析收藏纠错 + 选题
23. (2020九上·六安期末) 如图，直线y= $\text{[math]}$ x+ $\text{[math]}$ 与x轴交于点A，与y轴交于点C，以AC为直径作⊙M，点D是劣弧AO上一动点（D点与A，C不重合）．抛物线y=－ $\text{[math]}$ x²+bx+c经过点A、C，与x轴交于另一点B，
1. （1）求抛物线的解析式及点B的坐标；
2. （2）在抛物线的对称轴上是否存在一点P，是︱PA—PC︱的值最大；若存在，求出点P的坐标；若不存在，请说明理由．
3. （3）连CD交AO于点F，延长CD至G，使FG=2，试探究当点D运动到何处时，直线GA与⊙M相切，并请说明理由．
答案解析收藏纠错 + 选题