![]()

①小康同学:当t=2时,点P和点Q重合.
②小柔同学:当t=6时,点P和点Q重合.
③小议同学:当t=2时,PQ=8.
④小科同学:当t=6时,PQ=18.
以上说法可能正确的是( )

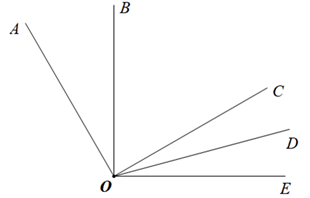
已知,如图,∠AOC=∠BOE=90°,OD是∠COE的角平分线,且∠DOE=15°.请你求出∠AOB的度数.
解:因为∠AOC=∠BOE=90°,
即∠AOB+∠BOC=90°,
∠BOC+∠COE=90°,
所以∠AOB与∠BOC互余,
∠BOC与∠COE互余.
所以∠=∠.(理由:)
因为OD是∠COE的角平分线,
所以∠COE=2∠.(理由:)
因为∠DOE=15°,
所以∠COE=30°.
所以=.
小明:你俩只要帮我讲讲解此方程第一步的想法、依据就可以了.
小丽:解此方程的第一步,应该先判断运算对象,我观察到含有括号,我认为应该先,依据是,就可以考虑其它变形,将方程变为x=a的形式.
小飞:解此方程的第一步还可以这样想,我观察到此方程含分母,我认为应该先,在方程两边都,依据是,也可以将方程变为x=a的形式.
①小明利用小丽的想法写出解此方程的第一步;
②小明利用小飞的想法写出解此方程的第一步.

①连接AB,点C在点B北偏东30°方向上,且BC=2AB,作出点C(保留作图痕迹);
②在(1)所作图中,D为BC的中点,连接AD,AC,画出∠ADC的角平分线DE交AC于点E;
③在①②所作图中,用量角器测量∠BDE的大小(精确到度).
|
购票张数 |
1~30张 |
31~60张 |
60张以上 |
|
每张票的价格 |
15元 |
12元 |
10元 |
原计划三个班都以班为单位购票,则一共应付1365元.三个班各有多少人?
例如:数轴上点A,B,C所表示的数分别为1,2,4,此时点B是点A,C的“2倍和谐点”;
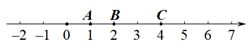


①若点Q是点A,C的“4倍和谐点”,求此时点Q表示的数;

②若点Q在点A的右侧,且点Q是点A,C的“n倍和谐点”,用含有n的式子直接写出此时点Q所表示的数.