 B .
B .  C .
C .  D .
D . 
|
成绩/次 |
150 |
160 |
168 |
170 |
175 |
178 |
180 |
|
人数 |
1 |
5 |
4 |
6 |
4 |
8 |
4 |
该班学生跳绳成绩的众数与中位数分别为( )
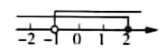 B .
B . 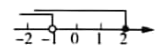 D .
D . 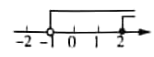
① 且
;②
;③
;④
;⑤直线
与抛物线
两个交点的横坐标分别为
,则
.其中正确的个数有( )
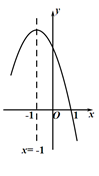
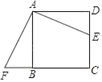


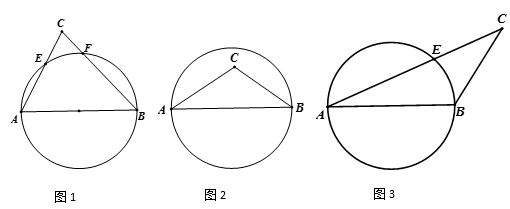

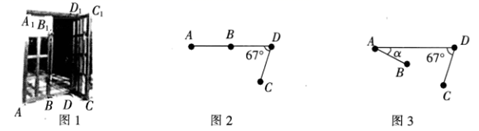

如图(2),当n=1时,BM与PD的数量关系为,CN与PD的数量关系为.
如图(3),当n=2时,矩形AMNP绕点A顺时针旋转,连接PD,则CN与PD之间的数量关系是否发生变化?若不变,请就图(3)给出证明;若变化,请写出数量关系,并就图(3)说明理由.
在(2)的条件下,已知AD=4,AP=2,当矩形AMVP旋转至C,N,M三点共线时,请直接写出线段CN的长
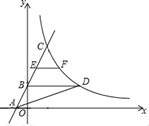
抛物线
与x轴的交点坐标为.顶点坐标为.请写出抛物线y,
的一条相同的性质.