 B .
B .  C .
C .  D .
D . 
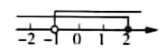 B .
B . 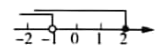 D .
D . 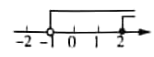


⑴将沿y轴方向向下平移4个单位长度得到
, 画出
并直接写出点
坐标;
⑵将绕着点O逆时针旋转
, 画出旋转后得到的
;
⑶直接写出点 ,
的坐标.
下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
|
型号 |
载客量 |
租金单价 |
|
A |
30人/辆 |
400元/辆 |
|
B |
20人/辆 |
300元/辆 |
注:载客量是指不包括驾驶员的每辆客车最多载客人数.学校租用A型号客车x辆,租车总费用为y元.
例如:分解因式;例如求代数式
的最小值.由
可知,当
时,
有最小值,最小值是
.
根据阅读材料用配方法解决下列问题;